Polygon Clipping

[wtosh]

/
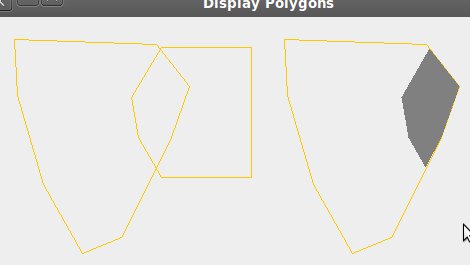
//  Clipper.java
//  
//
/**
 * Object for performing clipping
 *
 */

public class clipper {

    /**
     * clipPolygon
     * 
     * Clip the polygon with vertex count in and vertices inx/iny
     * against the rectangular clipping region specified by lower-left corner
     * (x0,y0) and upper-right corner (x1,y1). The resulting vertices are
     * placed in outx/outy.  
     * 
     * The routine should return the with the vertex count of polygon
     * resultinhg from the clipping.
     *
     * @param in the number of vertices in the polygon to be clipped
     * @param inx - x coords of vertices of polygon to be clipped.
     * @param int - y coords of vertices of polygon to be clipped.
     * @param outx - x coords of vertices of polygon resulting after clipping.
     * @param outy - y coords of vertices of polygon resulting after clipping.
     * @param x0 - x coord of lower left of clipping rectangle.
     * @param y0 - y coord of lower left of clipping rectangle.
     * @param x1 - x coord of upper right of clipping rectangle.
     * @param y1 - y coord of upper right of clipping rectangle.
     *
     * @return number of vertices in the polygon resulting after clipping
     * 
     */
    public float intersectX;
    public float intersectY;
    public float clipXmin;
    public float clipYmin;
    public float clipYmax;
    public float clipXmax;
    public int clipBorder;

    public int clipPolygon(int in, float inx[], float iny[], float outx[],
                float outy[],  float x0, float y0, float x1, float y1)
    {
        int numberOfVerticies = 0;
        int n;

        float Lx,Ly,Cx,Cy;

        Lx = inx[in-1];
        Ly = iny[in-1];

        for (n = 0; n < in; n++){
            Cx = inx[n];
            Cy = iny[n];



        if(isInside(Cx, Cy, clipBorder)){
            if(isInside(Lx,Ly,clipBorder)){
                outx[numberOfVerticies] = Cx;
                outy[numberOfVerticies] = Cy;
                numberOfVerticies++;


            }
            else{
                isIntersect(Lx,Ly,Cx,Cy,clipBorder);
                outx[numberOfVerticies] = intersectX;
                outy[numberOfVerticies] = intersectY;
                numberOfVerticies++;
                outx[numberOfVerticies] = Cx;
                outy[numberOfVerticies] = Cy;
                numberOfVerticies++;


            }
        }
        else{
                if(isInside(Lx,Ly,clipBorder)){
                    isIntersect(Lx,Ly,Cx,Cy,clipBorder);
                    outx[numberOfVerticies] = intersectX;
                    outy[numberOfVerticies] = intersectY;
                    numberOfVerticies++;

                    }
                }
            Lx = Cx;
            Ly = Cy;


            }
        return numberOfVerticies; // should return number of verricies in clipped poly.
    }



public boolean isInside(float newX, float newY, int clipBorder){
    if(clipBorder == 0 && newY > clipYmin){
        return true;
    }
    else if(clipBorder == 1 && newX > clipXmin){
        return true;
    }
    else if(clipBorder == 2 && newY < clipYmax){
        return true;
    }
    else if (clipBorder == 3 && newX < clipXmax){
        return true;
    }
    return false;
}
public void isIntersect(float x0, float x1, float y0, float y1, int clipBorder){
    float xDifference = x1 -x0;
    float yDifference = y1 - y0;

    if(xDifference == 0 || yDifference == 0){

        if(clipBorder == 0){
            intersectX = x0;
            intersectY = clipYmin;
        }
        else if(clipBorder == 1){
            intersectX = clipXmin;
            intersectY = y0;
        }
        else if(clipBorder == 2){
            intersectX = x0;
            intersectY = clipYmax;
        }
        else if(clipBorder == 3){
            intersectX = clipXmax;
            intersectY = y0;
        }
        return;
    }
    if(clipBorder == 0){

        //intersectX = x0 + ((((((int)xDifference) * ((int)clipYmin - (int)y0))<<8) / ((int)yDifference))>>8);
        intersectX = x0 + ((clipYmax - y0)/(y1-y0/x1-x0));
        intersectY = clipYmin;
    }
    else if(clipBorder == 1){
        intersectX = clipXmin;
        intersectY = (y1-y0/x1-x0)*(clipXmax-x0) + y0;
        //intersectY = y0 + ((((((int)yDifference) * ((int)clipXmin - (int)x0))<<8) / ((int)xDifference))>>8);  
    }
    else if(clipBorder == 2){
        //intersectX = x0 + ((((((int)xDifference) * ((int)clipYmax - (int)y0))<<8) / ((int)yDifference))>>8);
        intersectX = x0+((clipYmin-y0)/(y1-y0/x1-x0));
        intersectY = clipYmax;
    }
    else if(clipBorder == 3){
        intersectX = clipXmax;
        //intersectY = y0 + ((((((int)yDifference) * ((int)clipXmax - (int)x0))<<8) / ((int)xDifference))>>8);  
        intersectY = (y1-y0/x1-x0)*(clipXmax-x0) + y0;
    }
}

}

The main and the other classes are in this download.
http://www.megafileupload.com/en/file/383064/cg1-clip-zip.html

[wtosh]

This is the result should look like.

[Ezzaral]

And... ?
You haven't posted a question.

[wtosh]

What am I doing wrong? I can't seem to get it clip the polygon at all.

[bguild]

I don't know exactly why it doesn't work, but I can see some things which you are doing wrong. Your clippers instance variables are being used like global variables to the algorithm instead of using them in a proper object-oriented way, and that just makes your algorithm hard to understand and debug. Why are they all public? What is the exact purpose of each of them? Why do you keep testing the value of clipBorder when apparently nothing in your code ever changes its value? Since it's a public, we can't be sure just how or why its value might change.

You should rewrite your algorithm so that clipper has no instance variables. It apparently does nothing but implement the algorithm, and there is no need for any global variables for that algorithm. If you simplify it, it will become easier for you to spot any problems. If you find yourself wanting instance variables, I suggest they should be private final variables, set in the constructor and used as input to the algorithm. That can be done safely without confusing anything, and it would allow you to cut down the number of arguments to your methods.

[wtosh]

Which one are the instance variables?

[Taywin]

OK, I will try to explain your algorithm from reading your code.

1. You pass in a set of vertices from v0 up to v(n-1) where n is the total number of vertices. The v0 and v(n-1) are connected.
2. You start it from Lx,y [v(n-1)] and Cx,y [v0].
3. If point Cx,y is inside the clipping area
   3.1 if Lx,y is also inside the clipping area, the Cx,y is a part of new polygon (clipped polygon).
   3.2 else the line created by Cx,y and Lx,y should intersect with the clipping border. Obtain the intersection point and add both Cx,y and the intersected point to the new polygon.
4. Else if point Lx,y is inside the clipping area, then there should be an intersection point. Obtain the point and add to the new polygon
5. Lx,y is not Cx,y
6. Cx,y is the next vertex in the list
7. Go back to #3

Problem: You have the values of clipping area (x0,y0) to (x1,y1) but you never use them. You used only clipping border (pass to the isIntersect() or isInside()). I am guessing that clipBorder has 4 values -- 0 is top edge, 1 is right edge, 2 is bottom edge, and 3 is left edge. If you do not use the passing in rectangle clipping points, you are comparing NOTHING.

PS: isIntersect() should return the intersection point instead of placing it in the class's variables -- intersectX & intersectY. Because of doing so, it is really difficult to follow.

PSS: I am not sure whether your isIntersect() and isInside() methods are correctly implemented (in term of algorithm). The isInside() needs to check whether one of the clipping point is on the inner side of the polygon. You passed in only 2 vertices (and even with more variables of the clipping area points), you can't really determine whether it is inside or outside. You NEED to know what your polygon looks like. I believe that this assignment is a simple one because it expects only convex polygons to be clipped. If the polygon is a convex, you will need to test the point with all polygon edges and determine that it is result in the same value (negative or positive). If the polygon is not a convex, you will have a lot more to do in testing. The isIntersect() is simple, but you need 4 points (2 end-points of 2 lines). What you are doing right now is wrong, simple...

[bguild]

Actually, I'm pretty sure that being convex is a red herring when you are clipping a polygon to a rectangle. Being convex is helpful for determining if a point is inside or outside, but since the rectangle is guaranteed to be convex we can use that and simply iterate over the edges and vertices of the polygon, checking and clipping each in turn. That would work just as well for a concave polygon as a convex polygon.

[wtosh]

:( Taywin, if what I am doing is simply wrong, guide me through the process please.

[Taywin]

That would work just as well for a concave polygon as a convex polygon.

Not really. The test for a point inside a concave polygon is a lot more difficult. If you don't get it, how about given an arbitrary point and a polygon, determine whether the point is inside the polygon. If the polygon is a convex, you simply test that the point is staying on the same side for all edges of the polygon (same test as testing if a point is inside a triangle). If it is a concave, you cannot do that because the point will be on the opposite side of some edges. As a result, you need a different algorithm which becomes more complex.

The problem is about given a convex (rectangle) to clip with a polygon. The polygon is not necessary to be a rectangle. Seeing picture from the attached image, I would assume that the other polygon must be a convex.

@wtosh, it will be quite a long explanation. First, you need to be able to test whether a point is inside a polygon. You may read this point in a triangle test. Once you implement that part, then you should implement a method to compute intersection point for 2 line segments (explanation on stackoverflow).

[wtosh]

upon reading it can you teach me how to do that? or is the algroirth in that link?

[Taywin]

For testing a point in a convex polygon (triangle), it explains how to test and derive the algorithm equation to be much simplier. For intersection point, the person explains how to find it (somewhat algorithm).

[bguild]

There is no reason to test whether a point is in a polygon. All you need to do is test for points inside rectangles. If you really think that testing for points being inside polygons is necessary, then please explain where those points are coming from. I can only guess that you mean the four corners of the rectangle, but surely that's not very useful.

Whether the polygon is convex or concave, all you have to do is go along each vertex and edge in order. If the vertex is inside the rectangle include it, and if the next vertex is also inside then include the edge, until you get to a vertext that is not inside, then you create a new vertex where the edge intersects the edge of the rectangle. Then you go through the next vertices until you get to one that is inside the rectangle again, do the edge intersection again, and connect up the vertices as necessary. Of course you also have to take care of the special case when an edge intersects two sides of the rectangle, but that can only happen when both vertices are outside the rectangle.

Connecting the interection points is the tricky part because there will always be two ways to do it, a short way and a long way, and it's not obvious how you can be sure which one to choose. You probably shouldn't just throw away the vertices that happen to be outside the rectangle; you should make note of which way around the rectangle they go so you can know how to connect the new vertices that you create when the polygon comes back to the rectangle.

[wtosh]

@bguild How would I convert what you said into code?

[bguild]

I've realized that it is an advantage if the polygon is convex. You don't need to determine if a point is inside the polygon, but clipping a concave polygon can result in more than one polygon, and if you can assume that the convex polygon has clockwise vertices then you can connect intersection points in the clockwise direction. Otherwise you would probably need to use a ray from one of the intersection points parallel to the side of the rectangle to decide which direction was the inside direction.

Instead of using two float[] arrays to represent the polygon, I would use a list of java.awt.geom.Point2D or some equivalent point class. I would also use a java.awt.geom.Rectangle2D to represent the rectangle instead of 4 float parameters. Rectangle2D already has a method for determining if a point is inside, but if I didn't have that because I was using a different rectangle class, then my first step would be to make that. Step two would be to make a method that takes two points and a rectangle, and assuming one point is inside and one point is outside, it returns the point at which the edge between the two points intersects the outline of the rectangle.

Then I would probably make a method that takes two points and a rectangle and returns a list of all the places where the edge between the points intersects the outline of the rectangle. That could be zero, one, or two places, but I would only use that method when both points are outside the rectangle, so the result would always be zero or two places.

I would create a private class for organizing my results, something like:

private final class Intersect {
    public final int edgeIndex;
    public final Point2D intersection;
    public final boolean isInward;
    public Intersect(int edgeIndex, Point2D intersection, boolean isInward) {
        this.edgeIndex = edgeIndex;
        this.intersection = intersection;
        this.isInward = isInward;
    }
}

Then I would write a method that takes a list of those, the polygon, and the rectangle, and returns a collection of lists of points. I would make use of a method that takes an Intersect, the polygon, and the rectangle and returns an instance of a private enum:

private enum Direction { CLOCKWISE, COUNTERCLOCKWISE }

It would do this by taking a line through the intersection point that is parallel to the outline of the rectangle and then iterating through the polygon to see how many times the other edges of the polygon intersect the line on either side of the intersection point. It should be even on one side and odd on the other side, unless we've done something wrong. Return the Direction of the side that is odd.

I would also want a method that takes a list of Intersects and sorts it into clockwise order around the outline of the rectangle. I expect the list of Intersects would start in either clockwise or counterclockwise order, but it is important to know which one, so a sorting is called for. (You might alternatively just compare the first two Intersects and then reverse the order of the list if necessary.) I would use java.util.Collections.sort to do the sorting, and I would define a java.util.Comparator something like this:

private final class OutlineOrder implements Comparator<Intersect> {
    private final Rectangle2D rectangle;
    public OutlineOrder(Rectangle2D rectangle) {
        this.rectangle = rectangle;
    }
    @Override
    public int compare(Intersect a, Intersect b) {
    ...
    }
}

I'll leave the details of determining which Intersect is further clockwise to you.

Then all we have to do is go through the list of Intersects in clockwise order until we find the first inward Intersect, and we start building up a list of vertices from the polygon. Each time we get to an outward Intersect we add its intersection point to the list and determine the next inward Intersect by using that method that returns CLOCKWISE or COUNTERCLOCKWISE above. If the next one is clockwise then we just continue, but if the next one is counterclockwise then we end this list of vertices, add it to the collection, and start a new list of vertices at the next clockwise inward Intersect.

I hope that helps.

[wtosh]

What goes in the compare() method and the Direction() method?

[bguild]

You're right, forget about compare and the sorting idea. That was a mistake; there is no good way to sort them reliably. The Intersects will come already sorted, but depending on the polygon they may be going clockwise or counterclockwise. So I would take the first inward Intersect and check that its direction is clockwise, and if it's not clockwise then go to the next Intersect which should be outward and clockwise, then reverse everything: reverse the order of the vertices of the polygon, reverse the order of the Intersects, turn every inward Intersect into an outward Intersect, and every outward Intersect into an inward Intersect. This means that the outward clockwise Intersect is now an inward clockwise Intersect and you can proceed clockwise from there.

You may have to play with these ideas a little bit to get them to work. I haven't tested this.

[wtosh]

Alright i'll try it. Let me know when you test it.

[Taywin]

I've realized that it is an advantage if the polygon is convex. You don't need to determine if a point is inside the polygon, but clipping a concave polygon can result in more than one polygon, and if you can assume that the convex polygon has clockwise vertices then you can connect intersection points in the clockwise direction. Otherwise you would probably need to use a ray from one of the intersection points parallel to the side of the rectangle to decide which direction was the inside direction.

You said it. ;) Actually clipping a concave polygon (with either a convex or concave) can result in more than 2 polygons but convex (with convex) can result in up to 2 polygons. That addes a lot of complexity.

There is no reason to test whether a point is in a polygon.
Whether the polygon is convex or concave, all you have to do is go along each vertex and edge in order.

That's a dangerous assumption by using only edges. Testing for edge intersection tells you only whether a polygon is completely inside or outside another polygon. If the cliping area is completely inside a selected polygon, the program will handle as if it does not touch the polygon at all.

[wtosh]

Alright, I tried your solution and I got stuck. I still don't understand what I should put in the compare method.