Equation with two unknowns -- where do I start?

[KatseasSAvvas]

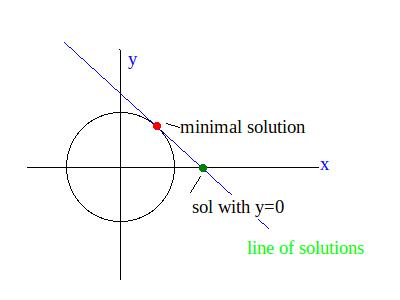
Hi, I'm trying to find a way to solve this equation with two unknowns using Python:

(a * b) = (x * c) + (y * d) + e

Where a, b, c, d and e are all floating numbers provided by the user and x and y are what the program should return. I'd really appreciate pointers to help me understand, some starting point if possible. Please bear in mind that my math is at the most basic level, I'd be totally helpless in front of a Wikipedia article on advanced algebra.

[slate]

You have to solve the equation first.

after some equivalent transformations:
y*d=a*b-e-x*c

If d==0 and c==0 then x,y can be anything if a*b-e==0 else nothing
if d==0 and c!=0 then y= anything, x=(a*b-e)/c
if d!=0 and c==0 then y=(a*b-e)/d, x is anything
if d!=0 and c!=0 then x,y can be an infinite number of pairs so that if x is given, then y= (a*b-e-x*c)/d

After that the program is pretty trivial.

[Gribouillis]

When one of c or d is not zero, the equation has an infinite number of solutions. In fact the solutions of x * c + y * d = f are

x = (f * c - z * d)/(c**2 + d**2)
y = (f * d + z * c)/(c**2 + d**2)

Here z can be any real number.
When c = d = 0, the equation has no solution if f is not zero, otherwise every pair (x, y) is a solution.

[KatseasSAvvas]

Thank you both for the suggestions. Let me define this a bit: I'm trying to calculate liquids. There is no chance of either c or d being 0.

From what you've suggested, it looks like there'd be infinite solutions. If what I'm looking for in the final solution is the smallest y possible, how should I tackle this?

Sidenote: please do share links to pages that will help me understand that sort of equations better if you happen to have them / know how to find them. My math is a mess, as I've already said, and when I'm searching for similar equations I just get confused by what I find.

[slate]

If c,d !=0 then any x,y pair that fulfill y= (a*b-e-x*c)/d is a solution. There is no minimum, since it is a linear function.

Maybe there are other prerequisites you did not share with us. Maybe some constraints on the domain of x or y, or some other equation x and y should conform...

[Gribouillis]

The solution

x = (f * c)/(c**2 + d**2)
y = (f * d)/(c**2 + d**2)

is minimum for the norm sqrt(x**2 + y**2). The set of solutions is a straight line in the plane (x, y) and this solution is the orthogonal projection of (0,0) on the line of solutions.

If you want to minimize y, there are 2 cases: if c == 0, then y is constant = f/d, if c != 0, the minimum for y is -infinity. If you want the minimal y >= 0, then you must chose x = f/c, y = 0.

[KatseasSAvvas]

I'll try researching the terms used before continuing this conversation. Thanks again!

[Gribouillis]

I'll try researching the terms used before continuing this conversation. Thanks again!

Here is a picture. The line can be anywhere in the plane.

[pyTony]

Maybe there is limit also for which numbers can be negative.