I see that there are many questions here regarding complexity analysis, specifically regarding the Big-O notation of algorithms. I will attempt to shed some light on the subject. I will start with an introduction, after which I will go over some common complexities and last we will solve a few simple examples for practice.
1. Introduction
When looking at the Algorithm, we want to know its order of growth regarding the input size given to it. Consider two simple algorithms that sort an array of [TEX]n[/TEX] cells. The first algorithm is doing [TEX]n[/TEX] operations in order to complete the sort, and the second algorithm is doing [TEX]n^2[/TEX] operations in order to complete it. If the array is of size [TEX]n=2[/TEX], then algorithm one would have done 2 operations while algorithm two would have done 4. When [TEX]n=10[/TEX] then algorithm one would have done 10 operations, and algorithm two 100 – see the difference? When talking about large values of [TEX]n[/TEX] (as in [TEX]{n\to\infty}[/TEX]) those differences will be much more significant – and we are talking just about the difference between [TEX]n[/TEX] and [TEX]n^2[/TEX], not mentioning [TEX]n^3[/TEX], [TEX]n^4[/TEX], and non-polynomial ones like [TEX]2^n[/TEX]!
This is what the Big-O notation is for – expressing the worst-case growth order of an algorithms given input data of size [TEX]n[/TEX]. Knowing if an algorithm can act as [TEX]n^2[/TEX] or at worst as [TEX]n[/TEX] can make big difference when choosing your algorithm or simply evaluating how good it is time-wise or space-wise.
This is the place to note that complexity can be evaluated by time-complexity or space-complexity. Time complexity is basically asking how much time or how many operations the algorithm did in proportion to [TEX]n[/TEX]. Space complexity is asking how much space – how many variables, array etc' have we used in proportion to [TEX]n[/TEX] in order to complete our mission.
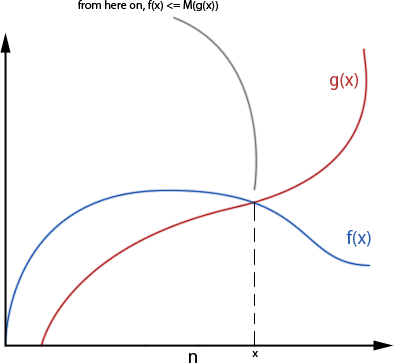
Saying it more formally (don't be alarmed - it's a little bit of math, and if you don't get it right away read along and it might be clearer later), saying that [TEX]f(x)[/TEX], our algorithm, is [TEX]O(g(x))[/TEX] if it holds that [TEX]|(f(x)| \leq M*|g(x)|[/TEX] for all [TEX]x>x0[/TEX]. It basically means that after a certain point, [TEX]f(x[/TEX]) will always be equal or smaller than [TEX]g(x)[/TEX], when looking on the absolute value. Using the examples from before, our first algorithm, the one that completes a sort of array of size [TEX]n[/TEX] in [TEX]n[/TEX] operations, will be [TEX]O(n)[/TEX] – since we can take [TEX]M=1[/TEX] and get [TEX]algorithm(n) \leq O(n)[/TEX] for every [TEX]n[/TEX].
2. Common O's In the programming world you will encounter some Big-O notations more than others. To give you some idea about a notation when you see one, here are the most notorious ones. Note – I will be writing it as time-complexity, but the space complexity is completely identical, just with different examples.[TEX]O(1)[/TEX] – The friendliest of the bunch. [TEX]O(1)[/TEX] basically means a constant time, with no regard to the given input size. Give it an array of size 20 or array of size 20,000, it will return after the same amount of operations. An example for such an algorithm is a function which excepts an array and returns its first element.
public int returnFirstElement(int[] arr)
{
return arr[1];
}3. Some practice
Now, enough talk, let's analyze! I will give you some brief examples that I've seen people struggle over in the forum.
A simple loop: Let's take this simple loop for our first example:
public void printMessage(int n)
{
for(int i = 0; i < n; ++i)
{
print("woohoo! I am a loop!")
}
}For a given [TEX]n[/TEX], the algorithm will print [TEX]n[/TEX] time the message "woohoo! I am a loop1". Give [TEX]n[/TEX] – it will do [TEX]n[/TEX] operations, and by definition our algorithm has [TEX]O(n)[/TEX] complexity. Note that all the operations such as print, simple arithmetic such as addition, multiplication, division and subtraction are always considered to be [TEX]O(1)[/TEX].
Two simple loops: Let's take a nested loop as our next example:
public void printMessage(int n)
{
for(int i = 0; i < n; ++i)
{
print("woohoo! I am the outer loop!")
for(int j = 0; j < n; ++j)
{
print("woohoo! I am the inner loop!")
}
}
}The outer loop goes from 1 to n, total of [TEX]n[/TEX] iterations. In each of the outer loop iterations, when we reach line 3, we enter another loop, also going from 1 to n, total of [TEX]n[/TEX] iterations as well. This means that for every outer iteration, the inner loop is doing [TEX]n[/TEX] iterations. For [TEX]n[/TEX] outer iterations, each one of them the inner loop is doing [TEX]n[/TEX] iterations we have [TEX]n*n=n^2[/TEX] iterations for a given [TEX]n[/TEX], making the complexity of the algorithm [TEX]O(n^2)[/TEX].
Different increments: Let's see another loop:
public void printMessage(int n)
{
for(int i = 0; i < n; i+=2)
{
print("woohoo! I am a loop!")
}
}This loop also prints the happy message, but every loop iteration I jumps by two and not by 1, meaning in the first iteration [TEX]i=1[/TEX], the second iteration [TEX]i=3[/TEX], third one [TEX]i=5[/TEX] and so on until [TEX]i=n[/TEX]. i will reach [TEX]n[/TEX] twice as fast now, instead of [TEX]n[/TEX] steps only at [TEX]\frac{n}{2}[/TEX] steps. So, what is the complexity? It is still [TEX]O(n)[/TEX] like when the increment was only by 1!. Let's remember what [TEX]O(n)[/TEX] means – it means that there exists a constant [TEX]M[/TEX] such that the [TEX]algorithm \leq M*n[/TEX]. In our case [TEX]M=\frac{1}{2}[/TEX] and we still get that the algorithm is [TEX]\leq \frac{1}{2}[/TEX], exactly what we want. It doesn't matter if the increments were by 1,2,5 or 20 – a constant does not change the complexity!
Another different increment: So, we have seen that increments by 1, 2, or 200 does not change the complexity, what about this loop:
public void printMessage(int n)
{
for(int i = 0; i < n; i*=2)
{
print("woohoo! I am a loop!")
}
}This time i doubles itself each iteration. This is not the same as constant increments- the first iteration [TEX]i=1=2^0[/TEX], the second iteration [TEX]i=2=2^1[/TEX], third iteration [TEX]i=2*2=2^2[/TEX], fourth iteration [TEX]i=2^3[/TEX]. After k iteration [TEX]i=2^{(k-1)}[/TEX]. After [TEX]x[/TEX] iterations [TEX]i=n[/TEX], let's see the value of x: after x iterations [TEX]i=2^{(x-1)}=n \Longrightarrow x=log(n) + 1[/TEX]. Since the "1" is constant time we can throw it away, since it does not affect the overall complexity of the algorithm. We get that the complexity then is [TEX]O(log(n))[/TEX].
4. Credit goes where credit is due
In order to write this introduction I have used A Beginners’ Guide to Big O Notation by Rob Bell and the Wikipedia Entry . A lot of thanks goes to ~s.o.s~ for commenting and helping me to make this intro better.
I hope that this little introduction made the complexity a little bit simpler. If you have any more questions or you have more helpful examples, please comment.