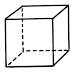
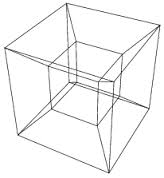
My math professor in the past explained it this way:
Consider yourself a 2D creature(some sort of pancake). If placed in a circle, you can't escape in a 2D world.
But in a 3D world this is simple. You could just jump up and disappear and reappear before all your 2D friends outside of the circle.
Now consider yourself a 3D creature(some sort of meatball). If placed in a sphere(football?), you can't escape in a 3D world.
In 4D, just "jump" and reappear on the outside!
Anyone any thoughts about this?
Or a better explanation?
ddanbe 2,724
Professional Procrastinator Featured Poster
Recommended Answers
Jump to PostI like that question!
The idea your trying to explain is a geometrical interpretation of a 4th dimention. There are plenty of other interpretations of it. Perhaps it would be better to first explain what dimentions are in mathemtatics before adding he symantics of space.
You already know that a …
Jump to Post4th dimension is "time" and we can not jump it.
If a one starts running his vehicle at the speed of light and one
starts chasing him after 2 hours at the speed of light, there will
always be a gap of 2 hours.
Jump to PostThe time dimension
4th dimension is "time" and we can not jump it.
Yet:
have to be careful we don't travel through occupied spaces
Jump to PostI dont have that book, I'll buy it tomorrow, and read it yesterday
Jump to Posttime as a fourth dimension is simple to understand
a floor plan is a section across the z dimension, and the time dimension
an elevation is a section across the x dimension, and the time dimension
or elevation is a section across the y dimension, and the time dimension
your …
All 53 Replies
pritaeas 2,194
¯\_(ツ)_/¯ Moderator Featured Poster
Hiroshe 499
Posting Whiz in Training
mattster
commented:
Someone has obviously studied their maths aha +0
mHealth 0
Newbie Poster
Reverend Jim 4,780
Hi, I'm Jim, one of DaniWeb's moderators. Moderator Featured Poster
ddanbe 2,724
Professional Procrastinator Featured Poster
Hiroshe 499
Posting Whiz in Training
Gribouillis 1,391
Programming Explorer Team Colleague
almostbob 866
Retired: passive income ROCKS
ddanbe
commented:
Great! :o) +0
jwenting 1,889
duckman Team Colleague
vegaseat 1,735
DaniWeb's Hypocrite Team Colleague
vegaseat 1,735
DaniWeb's Hypocrite Team Colleague
GrimJack 1,414
Posting Maven Featured Poster
GrimJack 1,414
Posting Maven Featured Poster
Reverend Jim 4,780
Hi, I'm Jim, one of DaniWeb's moderators. Moderator Featured Poster
almostbob 866
Retired: passive income ROCKS
Reverend Jim 4,780
Hi, I'm Jim, one of DaniWeb's moderators. Moderator Featured Poster
vmanes 1,165
Posting Virtuoso
Ketsuekiame 860
Master Poster Featured Poster
Reverend Jim 4,780
Hi, I'm Jim, one of DaniWeb's moderators. Moderator Featured Poster
GrimJack 1,414
Posting Maven Featured Poster
kplcjl 17
Junior Poster
kplcjl 17
Junior Poster
ddanbe 2,724
Professional Procrastinator Featured Poster
GrimJack 1,414
Posting Maven Featured Poster
GrimJack 1,414
Posting Maven Featured Poster
kplcjl 17
Junior Poster
ddanbe 2,724
Professional Procrastinator Featured Poster
Stuugie 50
Marketing Strategist
Reverend Jim 4,780
Hi, I'm Jim, one of DaniWeb's moderators. Moderator Featured Poster
Be a part of the DaniWeb community
We're a friendly, industry-focused community of developers, IT pros, digital marketers, and technology enthusiasts meeting, networking, learning, and sharing knowledge.