Simple Example of a Genetic Algorithm

Reverend Jim 2 1K Views

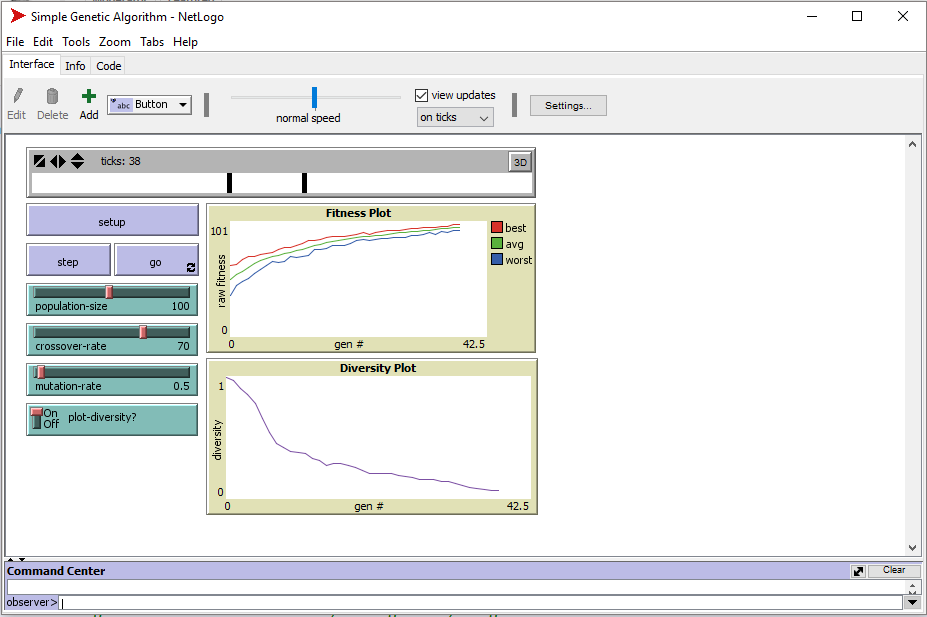
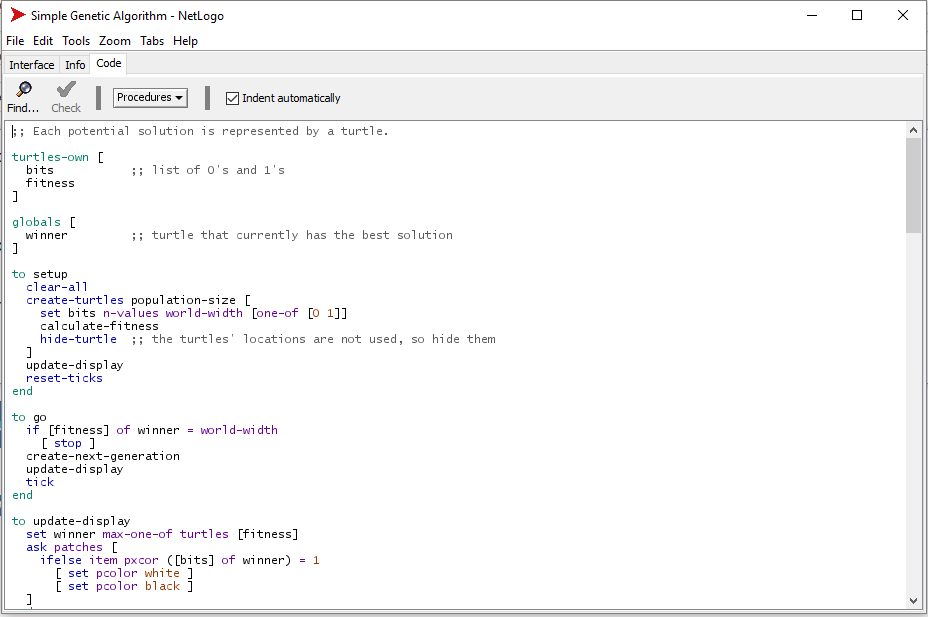
A while back I came across an article that mentioned genetic algorithms. For those unfamiliar with the term, simply put, rather than finding a solution to a problem by iterating over all possible cases, a genetic algorithm attempts to find a solution by starting with a guess, then generating a next guess by applying numerous random changes to the current guess and picking the guess that best fits the solution as the next best guess. Rinse and repeat.

Unfortunately, most of the articles and examples I came across involved far too much tech speak and math for a brain long removed from theoretical mathematics. I put it aside for a while until I read a paper by Richard Dawkins. He discussed the "Methinks it is like a weasel" algorithm in such clear terms that I coded it up in vbScript. It is such a simple example of a genetic algorithm that I decided to post it here.

In basic terms we define a target which is the string, "METHINKS IT IS LIKE A WEASEL". We generate ten new strings by applying a random mutation to the parent string. A mutation consists of possibly replacing a randomly selected letter with a new randomly generated letter. From the ten children we select the child that is the closest match to the target string. This child becomes the new parent for the next generation. If you run the script you will see how quickly we resolve to the target string.

Prior to running this script you should set cscript.exe as the default script engine by typing

cscript //h:cscript //s

otherwise each wscript.echo will pop up a message box. If you do not want to reset the default then run the script by

cscript weasel.vbs

This script uses only upper case letters and spaces but could be modified to include lower case letters and punctuation.

'																		'
'	Name:																'
'																		'
'		Weasel.vbs														'
'																		'
'	Description:														'
'																		'
'		Based on an algorithm by Richard Dawkins, this script uses a	'
'		genetic algorithm to generate a string that matches a given		'
'		string.															'
'																		'
'		The target string is given by <Target>. The first approximation	'
'		is generated at random. Each new generation consists of ten		'
'		"children" strings in which one letter may or may not have been	'
'		mutated (replaced by a randomly chosen letter). The next best	'
'		guess, or "Parent" is chosen by selecting the child that is the	'
'		closest match to the target string.								'
'																		'
'	Audit:																'
'																		'
'		2016-07-02	rj	modified from published code					'
'																		'

'This is the string we want to "evolve" to. Any string of any length will
'do as long as it consists only of upper case letters and spaces.

Target  = "METHINKS IT IS LIKE A WEASEL"

'This is the pool of letters that will be selected at random for a mutation

letters = " ABCDEFGHIJKLMNOPQRSTUVWXYZ"

'A mutation rate of 0.5 means that there is a 50% chance that one letter
'will be mutated at random in the next child

mutation_rate = 0.5

'Set for 10 children per generation

Dim child(10)

'Generate the first guess as random letters

Randomize
Parent = ""

for i = 1 to len(Target)
	Parent = Parent & Mid(letters,Random(1,Len(letters)),1)
next

'Create successive generations until target is reached

Do
	bestfit = 0
	bestind = 0
	
	'make n copies of the current string and find the one
	'that best matches the target string
	
	For i = 0 to ubound(child)
	
		child(i) = Mutate(Parent, mutation_rate)

		fit = Fitness(Target, child(i))
		
		If fit > bestfit Then
			bestfit = fit
			bestind = i
		End If
		
	Next

	'Select the child that has the best fit with the target string

	Parent = child(bestind)
	Wscript.Echo parent, "(fit=" & bestfit & ")"
	
Loop Until Parent = Target

'apply a random mutation to a random character in a string

Function Mutate ( ByVal str , ByVal rate )

	Dim pos		'a random position in the string'
	Dim ltr		'a new letter chosen at random	'

	If rate > Rnd(1) Then
	
		ltr = Mid(letters,Random(1,len(letters)),1)
		pos = Random(1,len(str))
		str = Left(str, pos - 1) & ltr & Mid(str, pos + 1)

	End If
	
	Mutate = str
	
End Function

'returns the number of letters in the two strings that match

Function Fitness (ByVal str , ByVal ref )

	Dim i
	
	Fitness = 0
	
	For i = 1 To Len(str)
		If Mid(str, i, 1) = Mid(ref, i, 1) Then Fitness = Fitness + 1
	Next
	
End Function

'Return a random integer in the range lower to upper (inclusive)

Private Function Random ( lower , upper )
  Random = Int((upper - lower + 1) * Rnd + lower)
End Function
Member Avatar for Traevel
Traevel 216 Light Poster

Unfortunately, most of the articles and examples I came across involved far too much tech speak and math for a brain long removed from theoretical mathematics.

I relate to this.

Quite a few years ago I came across an excellent tool to experiment with models and algorithms called NetLogo. It has its own little scripting language and a lot of sample models. After you've set up your model you can easily change parameters with sliders and buttons to see the effects of the change. I've seen it make people enthusiastic of the field just by letting them watch the wolf/sheep predation model unfold.

On the topic of genetic algorithms; it has an example of the "all ones" problem. Basically given a random string like "101101100001" the goal is to get it to "111111111111" by the same proces you describe above.

netlogo.png
netlogo_code.png

As a possible expansion on your solution (consider it an afterthought on my end) there is also the possibility of including elitism. This way the best solutions can be preserved over generations, by including the parent(s) as a child into the next generation without mutations. It can drastically speed up the progress of the algorithm.

Member Avatar for Reverend Jim
Reverend Jim 4,966 Hi, I'm Jim, one of DaniWeb's moderators.

I'll add that change into my script. It's an obvious change in the event that no children are a better fit than the parent, however, to be fair, in real life evolution this would not be an option.

Member Avatar for Traevel
Traevel 216 Light Poster

That's true. I didn't mean to crack down on your script or anything, it was just something I noticed.

Dawkins is a classic. I can also strongly recommend The Computational Beauty of Nature by Gary Flake (ISBN 9780262062008). It's a good read, and relatively low on math, considering the topic.

I often heard the question why genetic algorithms are better than guessing over and over (I assume because that's what it sounds like). He has a marvelous bit on the sheer size of even the simplest problem. As a sample problem he starts with a string of 35 random letters and he wants to achieve a target string: furious green ideas sweat profusely (the book is full of funny references like that btw). With 26 letters and a space as the possible options that would make for a total of 27^35 possibilities for a 35 letter string. Or as he puts it: "assuming there are 2^80 electrons in the universe and that the universe is around 10 billion years old, then each electron would have to make 300 million guesses per second for the entire age of the universe before a correct guess was likely to be made". The genetic algorithm he describes gets the required string in 46 guesses. Powerful stuff!

Again, I was just happy to see this script up here! There can't be enough posts about AI on Daniweb if you ask me.

Edited by Traevel because: Spelling and sentence structure
Member Avatar for Web_4
Web_4 0 Newbie Poster

You may be interested in this article about
an analytical solution to Dawkins' Weasel algorithm
It shows that the split between the Homo and Pan genera happened billions of years ago according to the Weasel algorithm, while in reality it was only some million years ago...

Be a part of the DaniWeb community

We're a friendly, industry-focused community of developers, IT pros, digital marketers, and technology enthusiasts meeting, networking, learning, and sharing knowledge.

Edit Preview