This is a complete tutorial on creating a Deterministic Finite Automata (DFA) in Swift.
Go through the entire post to get familiar with all aspects of DFAs, and then implement your own DFA in Swift from scratch by following the steps given here. This will give you real-world experience on how to create such a thing.
What is a DFA?
A DFA is a mathematical model of computation used to classify the input strings that can be accepted by a finite state machine.
Once classified, these strings are translated into an accepting state or an accepting path. The set of all (accepting) paths through the graph defines the language accepted by the corresponding FSA, and also serves as its computational description. A deterministic finite automaton is a theoretical device consisting of a finite number of states, and transitions between possible states.
States are represented by one-dimensional "state space" which can hold either single character or even multi-characters classifying the range so for example if it holds ASCII codes then you can use this character classifier to get real-life examples like aaa, ab, abc,yyy you can find all this information in this excellent tutorial created by Tal Sus which is a gem of a tutorial from the perspective of sheer simplicity and ease. You'll understand that once you check it out.
What's so special about DFAs? The big idea behind using DFAs is that they are deterministic: if some state accepts an input string (or sequence of symbols), then any other run starting at the same state will also accept the very same input string.
Moreover, there exists an algorithm called "partial computation" to compute the set of states accepting an arbitrary given word with only polynomial-time complexity, i.e., much faster than when we try to do it for regular expressions with exponential time complexity.
The idea of a DFA helps you in that it is easier to design an algorithm for processing input strings than it is using regular expressions.
Representation of a DFA
A DFA can be represented by a directed graph where each node (or vertex ) represents a state and an arc or edge connects two nodes if they represent different states; edges typically have labels, which are either character sequences, numbers (representing some quantity), or pseudocode snippets (if we want to make our automata more general).
The "initial" state is denoted as Q0 and the "final" state as F. Every non-final node's outEdges list must be finite. Here is what the above theory means in actual code:
A DFA is a data type that you can use to perform pattern matching of strings. In order to create a DFA, we will need one state for each possible character in our alphabet. For example, if I want to match only lowercase letters "a" through "z", my automaton would have 26 states, including the initial and final states.
Every time we enter a new state (character), we can keep track of which characters were consumed, what the next character in our string is and whether or not we finished processing all characters in the string associated with this state. Once every letter has been matched on, return true or false depending on whether the user's entry was correct.
DFA in Swift
The implementation of a DFA in Swift is fairly simple. Here's how you can do it:
State
First, create a struct called "State" and set it as Equatable; since we want to be able to compare our states with their variables — a variable called "name" which we set to be of type String, and a variable called "isFinal" of type Bool.

Creating the State struct for the DFA
The name variable is obviously the main point of comparison for our states, but the Bool value is important so that our machine knows whether or not it has reached a final state.
Transition
Next, we create a struct called "Transition" where we define a transition as something that has a "fromState", an input character, and a "toState" — we set the fields of this struct accordingly.
A transition in a DFA from one state to another is called a run. A run has exactly one start state and at least two end states, the final state of the run being where the transition leaves off. The start state of a run is called the starting state, and the end states are called final states.

Defining the variables for our Transition struct
A run is said to be active from its starting state if it has not yet left this state. A run is said to be acceptable if the set of end states just after the starting state contains one specific terminal symbol. If there exists such an accepting run, the DFA is said to accept the language defined by this run. If no accepting run exists, a DFA is said not to accept any string from an alphabet of some specified size.
Creating the States of Our Machine
For pedagogical sense, we will hardcode the state of our DFA — but there are also multiple implementations wherein these states can be accepted from the user through I/O.
We will name our states S1-S4 as seen in the code block below. It is important that the second parameter of the constructor be a transition in a DFA from one state to another is called a run. A run has exactly one start state and at least two end states, the final state of the run being where the transition leaves off. The start state of a run is called the starting state, and the end states are called final states.
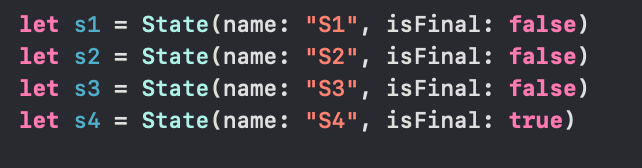
Hardcoding each state of the machine from S1-S4
A run is said to be active from its starting state if it has not yet left this state. A run is said to be acceptable if the set of end states just after the starting state contains one specific terminal symbol. If there exists such an accepting run, the DFA is said to accept the language defined by this run. If no accepting run exists, a DFA is said not to accept any string from an alphabet of some specified size.
ade clear which state/s are terminal states by setting the isFinal variable to “true”.
DFA Dynamics: Defining the Brain of Our Transitions
Finally, the last element of our DFA is what we will call our Transition Brain — where the logic behind our transitions is actually defined.
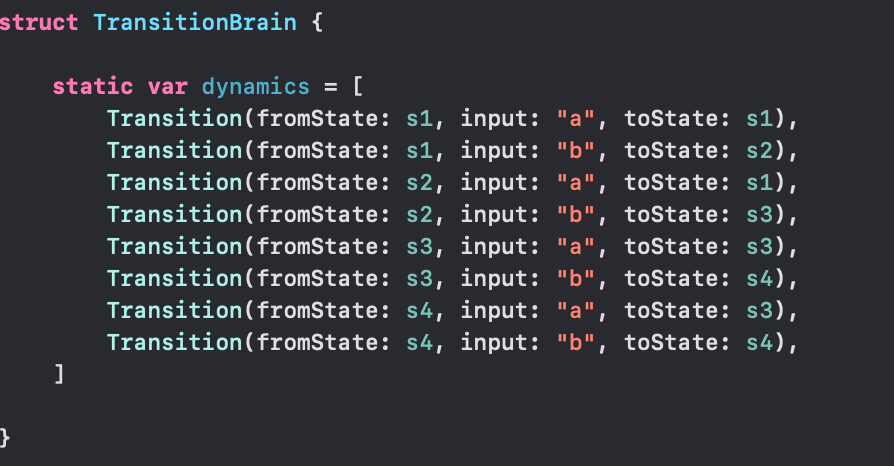
The TransitionBrain struct is the most important element
To do this, let’s create a struct called TransitionBrain, and inside it, we have a static variable called dynamics. The dynamics variable shall be a list of Transitions wherein each fromState, input, and toState is hardcoded.
Creating the Logic Behind the Automata
Now that we have the necessary elements for our deterministic finite machine, it is time to actually design the automata — including the functions that will control the behavior of our machine.
The first thing we have to do is create our initial state through a variable called currentState of type State. For simplicity, we will simply use s1 as our currentState. The functions of our automata are as follows:
Getting the Correct State
Our first state is a mutating function called getState — it does, as the name suggests, get the correct state that we are looking for based on the testInput that is passed as a parameter — called testInput of type String.
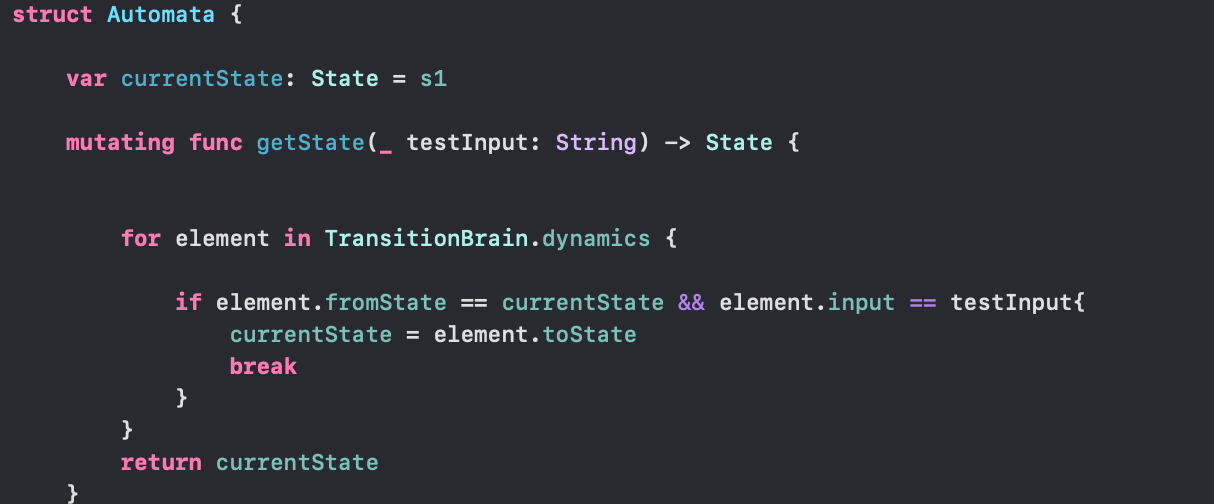
Creating our Automata struct, setting the initial currentState, and implementing getState
Through -> State, we make it clear that our function must return a State, or nothing at all. We then use an enhanced for loop to search for an element in the dynamics list of our TransitionBrain struct. It is worthy to note that each element will be of type State.
The logic behind this search is simple if the fromState of the current element of the for loop is equal to our currentState and the input value for the current element is equal to the current testInput value — we make a transition by setting the currentState to the toState of that element and then break the loop.
This function will then return the final value of the currentState variable.
Checking User Input for Validity
The final and most exciting part of Automata logic is where we actually check the user’s input String to see whether or not it is valid based on the transition rules of our DFA. We shall call this function checkString and have it return true if the input is acceptable, and false if it is not. Obviously, this will be a mutating function that takes in a String parameter.
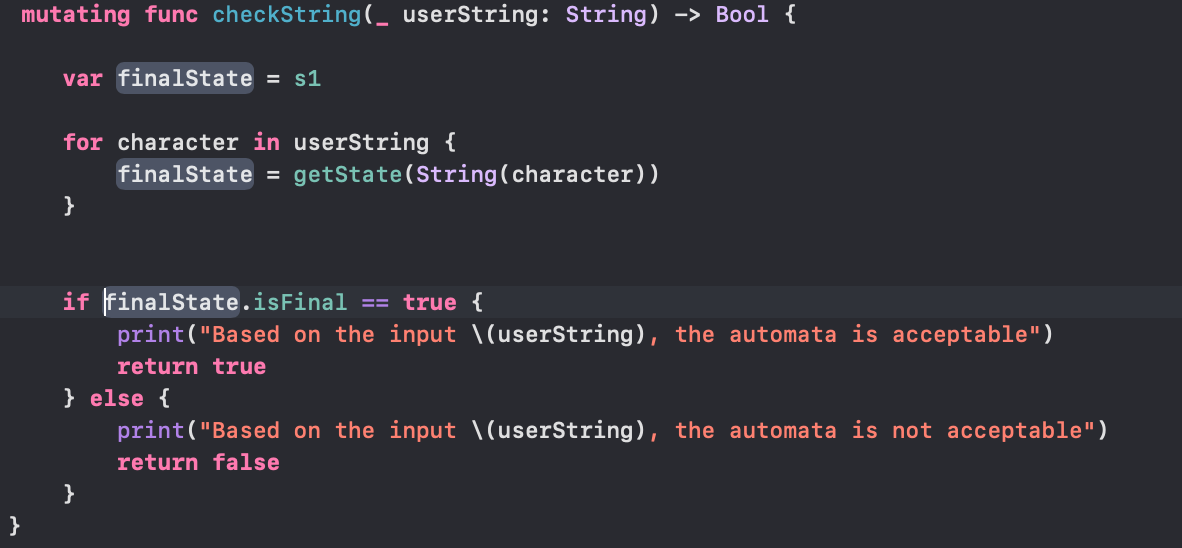
Checking if the user’s input is valid under the transition logic of our DFA
The first thing we have to do is create a placeholder finalState variable, we will set it to s1 but it actually does not matter what you set it to at this point.
Next, we do an enhanced for-loop on the user’s input and check every character, changing the value of our finalState variable based on our previously defined getState method with each character (typecast as String for syntactic validity) as the parameter value.
Once we arrive at the last finalState value, we output the name of the finalState with the line print("Final state is (finalState.name)").

A test run for our DFA
If the isFinal variable of the last state is true, then the String is acceptable under the transition rules of our automata.