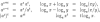Square Root Madness...

[KrazyKitsune]

This might be a little challenging, but I'd like to know.

from math import sqrt
y = int(raw_input("> "))
x = sqrt(y)
print x

In this code, say I input 4 for y. The output will be 2, naturally.
However, say I have 2 for y. I'd get something like 1.41421356.
Technically, sqrt(2) would be just sqrt(2).
And then say you have sqrt(48). In approximate decimal form, it is 6.92820323.
But I want to have Python think this as something like 4*(sqrt(3)) and print it as 4*(sqrt(3)) (or more preferably, 4%s3 where the % is the unicode symbol for the radical).

Erm... so, any help available?

[Gribouillis]

Here is a solution (I don't know if it's very robust): install the module sympy and

>>> from sympy import sqrt
>>> sqrt(48)
4*3**(1/2)

[TrustyTony]

Google for 'sympy python'

[KrazyKitsune]

AND Not using sympy. Sorry, but I can't download on my mac (I work cross platform). :/

[Gribouillis]

Also if you have linux or cygwin, install the pari CAS and pari-python and factor your number

>>> from pari import factor
>>> print factor(48, 48)

[2 4]

[3 1]

pari was written by number theorists. Use it for advanced arithmetic applications.

[Gribouillis]

AND Not using sympy. Sorry, but I can't download on my mac (I work cross platform). :/

What do you mean by 'I can't download on my mac' ? Can't you install any third party software ? Do you need a solution only with python's standard modules ?

[KrazyKitsune]

Err... yeah. Can we do it with only standard modules?

[Gribouillis]

Err... yeah. Can we do it with only standard modules?

Then use a naive partial factorization algorithm:

while n is even:
  divide n by two, collecting the number of times can it be divided by 2
for every odd number z starting from 1:
  if z ** 2 > n:
    break
  while z ** 2 divides n:
    divide n by z ** 2 and collect z ** 2 as a square divisor of n
You can now compute a and b such that the initial n = a * b ** 2
Print "b * sqrt(a)"

something like that.

[KrazyKitsune]

...I get what you mean, but I suck at converting text to python language.

[Gribouillis]

...I get what you mean, but I suck at converting text to python language.

It's what programming's all about :) We can't learn python for you, so show some effort.

[KrazyKitsune]

So you are saying this so far as far as I know:

So every time n is even, we divide n by two. The script then counts the number of times n can be divided by two.

But then I don't get the rest of it.

[TrustyTony]

(a**(2*n))**(1/2) == a ** n

[woooee]

It's what programming's all about We can't learn python for you, so show some effort.

For any newbies, this is the never-ending question technique. The OP keeps posting questions (with no effort at all) until someone is worn down enough to write the code for them. I don't care enough to check, but if you look at the OP's other posts you will probably see a similar style, so ignore this post, and this OP, as long as (s)he views us as code servants.

[KrazyKitsune]

(a**(2*n))**(1/2) == a ** n

....?

[TrustyTony]

....?

square root = raise to power 1/2
rule for multiplying the powers : ((a **m)**n) = a ** (m*n)

Hint: You can implement the processing of square roots as factoring by perfect squares of primes.

[KrazyKitsune]

square root = raise to power 1/2
rule for multiplying the powers : ((a **m)**n) = a ** (m*n)

Hint: You can implement the processing of square roots as factoring by perfect squares of primes.

...and?

Oh, I think I found a way.

I can find the prime factors of the number in the root, then (in my mind) use len() somehow to find how many of each number is under the root, and then finds all duplicates, takes one number from each duplicate and multiplies them all. Python then takes the leftover number and keeps it under the root. (Don't blame my math skills if I'm wrong)

But I don't know how to find ONLY duplicates, or for that matter, even decide how many of each number there is in the first place. :\

[TrustyTony]

Implement it, my code is 9 lines long as function, of course you need the list of primes also.

Luck with coding!

[KrazyKitsune]

Agh. I can't find the prime factors.

[KrazyKitsune]

Help?