Need help with backtracking in C

Hey guys, I'm really stuck on this problem. I think you have to do backward recursion, but don't know how to go about it. I just need help with the algorthim for the function "backtracking".

Find the best cheapest way to get from city 1 to city 2. I have already found the cheapest way by hand, which city1 -> city 2 -> city 5 -> city 8 -> city 10.

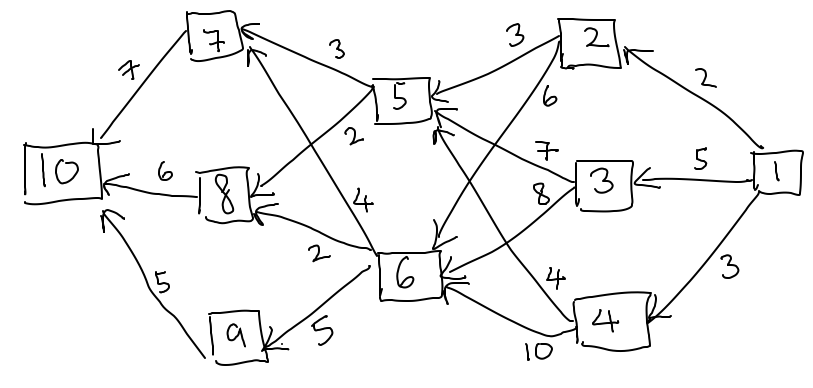
Here is a picture of the diagram ^

THANKS IN ADVANCED!!

Here is the code I have so far.

#include <stdio.h>


    int backTracking(not sure what to put here..)
    {
     //.....  
     }

    }
    int main (void)
    {
        //hard code all the prices
        int cityOneTwo = 2;
        int cityOneThree = 5;
        int cityOneFour=3;
        int cityTwoFive=3;
        int cityTwoSix=6;
        int cityThreeFive=7;
        int cityThreeSix=8;
        int cityFourSix= 10;
        int cityFourFive=4;
        int cityFiveEight=2;
        int cityFiveSeven=3;
        int citySixSeven=4;
        int citySixEight=2;
        int citySixNine= 5;

        int cost[4][9]; //make an array for day and city... day 1 includes city 1, day 2 includes city 2,3,4... and so on

        //day 4
        cost[3][6]=7; //intiallize cost from city 7 to city 10
        cost[3][7]=6; //intiallize cost from city 8 to city 10
        cost[3][8]=5; //intiallize cost from city 9 to city 10

        //day 3: city 5
        int wayFiveSeven=cityFiveSeven + cost[3][6];
        int wayFiveEight= cityFiveEight + cost[3][7];

        if (wayFiveSeven<wayFiveEight) 
            cost[2][4] = wayFiveSeven;
            else
                cost[2][4] = wayFiveEight;

        //day 3: city 6
        int waySixSeven= citySixSeven + cost[3][6];
        int waySixEight= citySixEight + cost[3][7];
        int waySixNine= citySixNine + cost[3][8];

        if (waySixSeven < waySixEight && waySixSeven <waySixNine)
            cost[2][5]= waySixSeven;
        else if (waySixEight < waySixSeven && waySixEight < waySixNine)
            cost[2][5] = waySixEight;
            else
            cost[2][5] = waySixNine;

        //day 2: city 4
        int wayFourFive = cityFourFive + cost[2][4];
        int wayFourSix= cityFourSix + cost[2][5];

        if (wayFourFive<=wayFourSix)
            cost[1][3]= wayFourFive;
        else
            cost[1][3]= wayFourSix;

        //day 2: city 3

        int wayThreeFive = cityThreeFive + cost[2][4];
        int wayThreeSix = cityThreeSix + cost[2][5];

        if (wayThreeFive <= wayThreeSix)
            cost[1][2]= wayThreeFive;
        else
            cost[1][2]= wayThreeSix;

        //day 2: city 2
        int wayTwoFive= cityTwoFive + cost[2][4];
        int wayTwoSix= cityTwoSix + cost[2][5];


        if (wayTwoFive <= wayTwoSix)
            cost[1][1]= wayTwoFive;
        else
            cost[1][1]= wayTwoSix;

        //day 1: city 1

        int wayOneTwo = cityOneTwo + cost[1][1];
        int wayOneThree = cityOneThree + cost[1][2];
        int wayOneFour = cityOneFour + cost[1][3];

        if (wayOneTwo < wayOneThree && wayOneTwo < wayOneFour)
            cost[0][0]= wayOneTwo;
        else if (wayOneThree < wayOneTwo && wayOneThree < wayOneFour)
            cost[0][0] = wayOneThree;
        else
            cost[0][0] = wayOneFour;

        //determine the total cost

        int totalcost= backTracking(not sure what to put here...);
        }

forgot to put return (0); between line 100 and line 101.

p.s its a backward dynamic program.

[L7Sqr]

Dynamic programming most times revolves around caching or memoization generally coupled with some sort of recursion. The idea in this case would look something like:

for each Node1 in Graph:
   set Node1 as Root.
   for each Node2 in (Graph - Node1):
      calculate ShortestPath(Root, Node2)

print ShortestPath(NodeA, NodeB)

The ShortestPath would be the recursive portion that would do the caching

ShortestPath(Root,Target)

   if exists CACHE[(Root,Target)]
      return CACHE[(Root,Target)]

   LowestCost = Infinity

   for Neighbor in Root.Neighbors:
      Cost = Cost(Root,Neighbor) + ShortestPath(Neighbor,Target)
      if Cost < LowestCost
         LowestCost = Cost

   CACHE[(Root,Target)] = LowestCost
   return LowestCost

The first iteration is the most costly as every call to ShortestPath requires you to do the full calculation. As you iterate over the nodes the cache fills up and by the last few nodes you have to do very little calculation since you've already traversed the entire graph.