In this tutorial I am going to go over a brief history of artificial intelligence. Let's begin.
The Beautiful Equation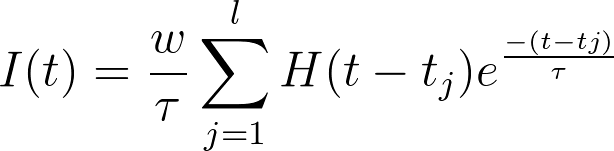
OK I agree, it's a bit heavy to begin with but towards the end we will see why the above equation is, in my opinion, of great importance to the field of AI. But first let's go back in time to ancient Greece.
Ancient Greece
The Greeks dreamt about artificial intelligence, playing God if you will, they probably weren't the first. But the idea of mechanically creating an intelligence to rival our own has always been on the frontier of science. And it is no surprise why... the human brain is an enigma, an amazing feat of biological engineering, capable of making complicated deductions and understanding subtle nuances. Clearly, no hard coded computer program can rival such mastery.
So our immediate question is... how do we recreate this? Do we follow nature as an example?
Mankind masters flight Mankind has always taken their inspiration from nature. For a long time mankind was hellbent on being able to fly. In Greek mythology Icaraus forges wings out of wax to give himself the ability to fly. It is just myth of course, but man's idea to emulate nature seems a good starting point. Many of the first flying contraptions devised tried to copy the flight of a bird by copying the flapping of the wings to generate lift. But no such devices ever succeeded. Mankinds first powered flight came from aerodynamic wings that were FIXED but provide thrust to create lift.
Mankind has always taken their inspiration from nature. For a long time mankind was hellbent on being able to fly. In Greek mythology Icaraus forges wings out of wax to give himself the ability to fly. It is just myth of course, but man's idea to emulate nature seems a good starting point. Many of the first flying contraptions devised tried to copy the flight of a bird by copying the flapping of the wings to generate lift. But no such devices ever succeeded. Mankinds first powered flight came from aerodynamic wings that were FIXED but provide thrust to create lift.
So we could say flight was achieved my not completely copying nature but rather taking ideas from it and changing a few things along the way.
Should the quest for AI then try to COMPLETELY copy how the brain works completely? Only time can answer this question. But I believe it is a damn good place to start.
Next we are going to explore the brain.
The Brain
The brain consists of literally millions of neurons. Each neuron are inter connected with synapses. These pass electrical signals to the neurons. Now an individual neuron by itself is pretty useless. Learning occurs by the collective information of all the neurons in the brain.
Basically, when a neuron fires it needs to be excited and once it reaches a threshold it fires an electrical signal. Think of it like a reward system. If the dog behaves it gets a treat. So in the same way when a neuron is learning, if the desired action is considered good enough (i.e it goes beyond some threshold value) it fires.
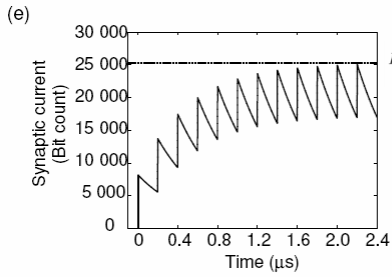
Now we can come back to our equation written at the beginning. All it does is describe the graph of a spiking neuron. The most important bit is that 'w' describes the 'weight' and in all neural networks learning occurs by continually adjusting the weights.
The downward slope of the graph is described by the exponentional function.
How do we replicate the spiking neuron graph?
So we have the graph of a neuron. Our next question is how might we replicate this? First we might think of this in software terms. You might write a program in say 'java' or 'C#' to replicate the graph. Now software is great but it is slow. What if we cloned the graph directly with hardware. Wouldn't that be faster?
Enter the FPGA
So what is an 'FPGA.' It is a 'Field programmable gate array.' Think of it like a bunch of logic gates that can be configured to how you like.
Why use an FPGA
Why? It's simple. FPGAs are fully Parallel. No shared resources mean no serial dependencies. Single Clock for cycle Numerical Iteration. One clock cycle equals one numerical iteration.
In short it is bloody fast and works much like a neuron. In parallel.
Problems with floating point calculation in hardware
Let's go back to our equation. Unfortunately, we've got exponential decay described in our graph. If you don't already know floating point calculations,or in our case differential/integral calculations perform horribly on hardware - (using logic gates).
So we employ a little trick which involves using the forward-euler method to approximate the exponential decay.
http://en.wikipedia.org/wiki/Euler_method
Let's not get too technical here, but essentially we use repeated subtraction to estimate exponential decay and remove the need for floating point calculations. Point to note, repeated subtraction can easily be constructed with logic gates.
So let's say we have now devised an FPGA for a neuron. The basic configuration to set up many in parallel will look as follows:-
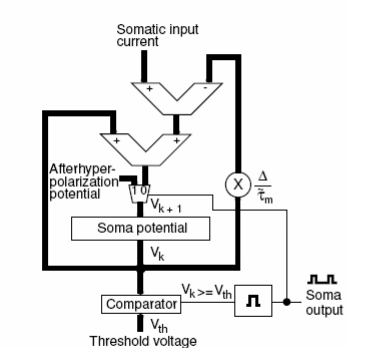
Conclusions
-Learning occurs by adjusting the weight matrix in a neuron
-A spiking neuron can be modelled with FPGAs which have the benefit of being massively parallel and having no serial depencies. This makes it much much faster than modelling in software.
-The forward-eular trick can be used to approxiate exponential decay thereby reducing the calculation computations.
Overall, this points us to the conclusion that modelling neural networks in hardware should offer more efficient and faster learning results.
Thanks for reading.
Further reading
If you are interested in getting setup, you can head over to http://www.xilinx.com/ and download their SDK. You can simulate your FPGA circuits with their software before buying the real thing (and flashing the hardware).
