Calculating a formula with complex numbers in it in C#

ddanbe 1 613 Views

One of the most, if not THE most, beautiful formulas in math, is from Euler: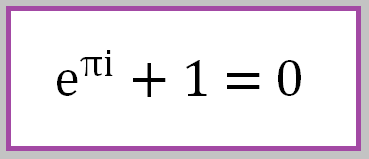
Euler_e_pi_i.png

It combines in it a relation between the number e, the number Pi and the complex number i, plus the basic math symbols 1, +, = and zero. Is that not amazing?
More info on this formula can be found here.
The Complex type in C# is available as of .NET v4.0 and lives in the System.Numerics namespace.
As this type is not used on a regular basis it is not included as reference in every project by default.
So you have to include that reference first. Don't forget to add using System.Numerics; to your .cs file either.
Enjoy!

using System;
using System.Numerics;

namespace Pi_e_i_formula
{
    class Program
    {
        static void Main(string[] args)
        {
            Console.WriteLine("Calculation of the formula e^Pi*i  + 1 = 0");
            Console.WriteLine();
            // Turn an int or double into (1 ,0) same as new Complex(1, 0) or Complex.One;
            Complex One = 1;
            Complex z = Complex.Exp(Complex.ImaginaryOne * Math.PI) + One;
            Console.WriteLine("Print calculation with no formatting.");
            Console.WriteLine(z.ToString());
            Console.WriteLine("Print calculation to 6 decimal places.");
            Console.WriteLine(z.ToString("F6"));
            
            Console.ReadKey();
        }
    }
}
Member Avatar for kplcjl
kplcjl 17 Junior Poster

I apparently haven't had the math education in the dark ages (1960s) that I thought I had. I know:
i^2 == -1
I haven't seen i used as an exponential value in any formula, but I've not studied Euler much either.
How in the world does 2.718 raised to power (3.14159 times i) come near -1? The only way I knew how to make an imaginary number into a real number was to multiply it by i and I thought a complex expression couldn't be made real.

PS I have free VS 2012, I thought I had .NET 4.?, but System doesn't know Numerics type.

Member Avatar for ddanbe
ddanbe 2,724 Professional Procrastinator

Yes, I had the same doubts as you with this formula, but in time I learned that complex and imaginary numbers act very differently than real and other numbers and that we still can very well work with them.

For the Numerics you could perhaps upgrading to the free VS 2015 will help?
I have VS 2008, 2010, 2013 and 2015.

For a derivation of this formula there is a lot to be found on the web.
But this video looks clear and instructive to me. Enjoy. :)

Member Avatar for JOSheaIV
JOSheaIV 119 C# Addict

Wow didn't even know this library existed. I wonder if it can help with the last piece I need for my RSA key generation? Having trouble with the Extended Euclidian Algorithm (it only wants to work part of the time, but if I produce to large or random numbers, then it doesn't produce my keys correctly)

Did you see that algorithm in that collection?

Edited by JOSheaIV
Member Avatar for ddanbe
ddanbe 2,724 Professional Procrastinator

Here is what it contains.
I think the BigInteger structure will interest you.

Member Avatar for JOSheaIV
JOSheaIV 119 C# Addict

Actually there is a part of RSA key generation that not even a BigInteger can handle. There was a specific formula that gets around the issue of trying to work with massive numbers (doubles can't even handle). I forgot what the exact name of the forumla was.

Unfortantly, it looks like this namespace does more geometry type stuff then anything (and maybe Linear Algebra and Calc since I see those Matrixes)

Member Avatar for ddanbe
ddanbe 2,724 Professional Procrastinator

In theory a BigInteger has no min or max value like the other integers.
Read about it here.

Member Avatar for JOSheaIV
JOSheaIV 119 C# Addict

I see. I did a quick google, it almost looks like it stores the value in a bit array. That theoretcially would allow for a rather large number (to an extent though, as long as the array doesn't exceed)

Be a part of the DaniWeb community

We're a friendly, industry-focused community of developers, IT pros, digital marketers, and technology enthusiasts meeting, networking, learning, and sharing knowledge.

Edit Preview