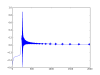
I programmed a a neural network class in python using numpy. I had some trouble getting it to work properly, in my case I wanted to train it with back propagation to approximate XOR, but then it started working, then it didn't, and overall it only seems to work sometimes. Just to be clear, what I mean is that at each step in back propagation I record the network's rms error and in the end I plot it, sometimes the error goes to zero and sometimes it gets hung up at about .85.
This is my code(I guess that makes this a python thread now, but I thought this might be a problem to do with neural networks in general.) I don't know how readable it is but if you have numpy and matplotlib then you can run it a few times and see what I mean.
import numpy
from matplotlib import pyplot
def sigmoid(x):
return numpy.tanh(x)
def dsigmoid(y):
return 1.0 - y**2
class ANN:
def __init__(self, dims):
self.activations = numpy.zeros((len(dims), max(dims)))
self.biases = numpy.random.random((len(dims), max(dims)))
self.weights = numpy.random.random((len(dims), max(dims), max(dims)))
self.dims = dims
self.num_layers = len(dims)
def run(self, inputs):
if len(inputs) != self.dims[0]:
raise ValueError, "Network expected " + repr(self.dims[0]) + " inputs but " + repr(len(inputs)) + " were given"
self.activations[0,:self.dims[0]] = inputs
for a in xrange(1, self.num_layers):
for b in xrange(self.dims[a]):
self.activations[a,b] = sigmoid(self.biases[a,b] + sum(self.weights[a,b,:self.dims[a-1]]*self.activations[a-1,:self.dims[a-1]]))
return self.activations[-1,:self.dims[-1]]
def back_propogation(self, inputs, outputs, iterations = 1, learning_rate = .5, momentum = .1):
if len(inputs) != len(outputs):
raise ValueError, repr(len(inputs)) + " inputs were given but " + repr(len(outputs)) + " outputs were given"
for a in xrange(len(inputs)):
if len(inputs[a]) != self.dims[0]:
raise ValueError, "Network expected " + repr(self.dims[0]) + " inputs but input " + repr(a) + " gives " + repr(len(inputs[a])) + " inputs"
elif len(outputs[a]) != self.dims[-1]:
raise ValueError, "Network returns " + repr(self.dims[0]) + " outputs but output " + repr(a) + " expects " + repr(len(inputs[a])) + " outputs"
mse = numpy.zeros(iterations)
deltas = self.biases*0
inertias = self.weights*0
bias_inertias = self.biases*0
for a in xrange(iterations):
for b in xrange(len(inputs)):
self.run(inputs[b])
error = outputs[b] - self.activations[-1,:self.dims[-1]]
mse[a] += sum(error**2)/len(error)
deltas[-1,:self.dims[-1]] = dsigmoid(self.activations[-1,:self.dims[-1]]) * error
for c in xrange(len(deltas) - 2, 0, -1):
error = numpy.zeros(self.dims[c])
for d in xrange(0, self.dims[c]):
error[d] = sum(deltas[c+1,:self.dims[c+1]]*self.weights[c+1,:,d])
deltas[c,:self.dims[c]] = dsigmoid(self.activations[c,:self.dims[c]]) * error
for c in xrange(len(deltas) - 1, 0, -1):
for d in xrange(self.dims[c]):
change = deltas[c,d]*self.activations[c-1,:self.dims[c-1]]
#print change
self.weights[c,d,:self.dims[c-1]] += learning_rate*change + momentum*inertias[c,d]
self.biases[c,d] += learning_rate*deltas[c,d] + momentum*bias_inertias[c,d]
inertias[c,d] = change
bias_inertias[c,d] = deltas[c,d]
return mse
a = ANN((2, 2, 1))
inputs = numpy.array([[0, 0], [0, 1], [1, 0], [1, 1]])
outputs = numpy.array([[0], [1], [1], [0]])
error = a.back_propogation(inputs, outputs, 1000)
print a.run(inputs[0])
print a.run(inputs[1])
print a.run(inputs[2])
print a.run(inputs[3])
pyplot.plot(error)
pyplot.show()