#include <iostream>
#include <conio.h>
using namespace std;
void TOH(int d, char tower1, char tower2, char tower3)
{
if(d==1) //base case
{
cout<<"\nShift top disk from tower"<<tower1<<"to tower"<<tower2;
return;
}
TOH(d-1,tower1,tower3,tower2); //recursive function call
cout<<"\nShift top disk from tower"<<tower1<<"to tower"<<tower2;
TOH(d-1,tower3,tower2,tower1); //recursive function call
}
int main()
{
int disk;
cout<<"Enter the number of disks:.";
cin>>disk;
if(disk<1)
cout<<"\nThere are no disks to shift";
else
cout<<"\nThere are "<<disk<<"disks in tower 1\n";
TOH(disk,'1','2','3');
cout<<"\n\n"<<disk<<"disks in tower 1 are shifted to tower 2";
return 0;
}`
/* Enter the number of disk:. 3
/* My understanding...from Main, TOH with its parameters are passed on to void TOH function, then the base case is checked, the if block is skipped as the condition fails since d is 3, then recursive function TOH(d-1 .......tower1) is called....after then I dont get what happens as the output of the function is confusing, more confusing is the argument change from cout function please help.*/
surfingturtle 0 Light Poster
Recommended Answers
Jump to PostThis is a classic problem in computer science. Basically it is a neat case of induction.
For towers named A,B,C:
Start with a tower of just 1 disk. Transferring it is as easy as moving it from A->C.If you have more than 1 disk its a bit more complicated. …
Jump to PostIts actually not changing num at all. Instead it creates a brand new version of num in the next function call, starting from scratch. You can picture recursive functions as infinite code like this:
void printNum(int num) { cout<<num; if (num<9) { printNum(num+1); } cout<<num; } //is …
All 8 Replies
turboscrew 0 Light Poster
Hanoi (disks, from_peg, to_peg, spare_peg)
if disks == 0 return
if disks is 1
{
move topmost disk from from_peg to to_peg
}
else
{
Hanoi(disks-1, from_peg, spare_peg, to_peg)
Hanoi(1, from_peg, to_peg, spare_peg)
Hanoi(disks-1, spare_peg, to_peg, from_peg)
}
Labdabeta 182 Posting Pro in Training Featured Poster
This is a classic problem in computer science. Basically it is a neat case of induction.
For towers named A,B,C:
Start with a tower of just 1 disk. Transferring it is as easy as moving it from A->C.
If you have more than 1 disk its a bit more complicated. Start my moving all but 1 disk to the extra peg. How? By following these same instructions! Next move the biggest disk onto the final peg. Next move all the other disks from the extra peg to the final peg. This can also be done by following the same steps. Now you are done!
The key is that you change which peg is the initial, final, and extra peg, then keep recursively moving smaller towers until all you need to do is move towers of 1 disk, which is easy!
This is exactly what your code does.
1 disk: if only 1 disk, then move it.
if (d==1)
{
cout<<"\nShift top disk from tower"<<tower1<<"to tower"<<tower2;
return;
}
n+1 disks:
Step 1: move n disks to extra tower (tower3), while doing this the final tower (tower2) acts as the extra tower.
TOH(d-1,tower1,tower3,tower2); //TOH(n,initial,final,extra)
Step 2: move 1 disk to final tower (tower2)
cout<<"\nShift top disk from tower"<<tower1<<"to tower"<<tower2;
Step 3: move n disks from the extra tower (tower3) to the final tower (tower2) using the initial tower (tower1) as the extra.
TOH(d-1,tower3,tower2,tower1);
So for d=3 you have: (using A,B,C as the towers)
TOH(3,A,B,C); //move 3 disks from A to B using C as extra
\- TOH(2,A,C,B); //move 2 disxs from A to C using B as extra
\- TOH(1,A,B,C); //move 1 disk from A to B using C as extra
\- A->B; //base case, move from initial to final
\- A->C; //recursive case, move from initial to final
\- TOH(1,B,C,A); //move 1 disk from B to C using A as extra
\- B->C; //base case, move from initial to final
\- A->B; //recursive case, move from initial to final
\- TOH(2,C,B,A); //move 2 pegs from C to B using A as extra
\- TOH(1,C,A,B); //move 1 disk from C to A using B as extra
\- C->A; //base case, move from initial to final
\- C->B; //recursive case, move from initial to final
\- TOH(1,A,B,C); //move 1 disk from A to B using C as extra
\- A->B; //base case, move from initial to final
Checking the terminal lines (the X->Y ones) where things actually happen you can see that it works!
A=1,2,3; B= ; C= ; //initial state
A=2,3 ; B=1 ; C= ; //state after A->B
A=3 ; B=1 ; C=2 ; //state after A->C
A=3 ; B= ; C=1,2; //state after B->C
A= ; B=3 ; C=1,2; //state after A->B
A=1 ; B=3 ; C=2 ; //state after C->A
A=1 ; B=2,3 ; C= ; //state after C->B
A= ; B=1,2,3; C= ; //state after A->B, final state!
ddanbe commented: For the effort :) +15
surfingturtle 0 Light Poster
turboscrew and labdabeta, thanks a lot for your support and prompt response, I appreciate it much.
Am learning (self study) C+++ from books written by Alen Alex and Yashwant Kanetkar, in both they have explained the Recursive function with good basic ideas, but when it comes to practical implementation, things goes for a toss leaving with very little clue.
From the explanations provided by you and from this website http://clanguagestuff.blogspot.in/2013/09/tower-of-hanoi.html I got the logic part how things actually work practically, but how the recursion takes over this action is still a bit mystery for me, maybe I need to dig further about the working of this unique function....I would like to present here my understanding of recursive function from the program I have gone through, please have a look at it to know my line of thoughts which I apply to understand how recursive function manoeuvre the "control flow"..
#include <iostream>
using namespace std;
void printNum (int num)
{
/* the two calls in this function to cout will sandwich an inner sequence containing the numbers (num+1)...99...(num+1) */
cout << num; //first call
/* While begin is less than 9, we need to recursively print the sequence for (num+1) ... 99 ... (num+1)
if ( num < 9 )
{
printNum( num + 1 ); //recursive function
}
cout << num; //second call
}
int main ()
{
printNum( 1 );
}
//output is 123456789987654321
//my understanding ...(please)....from main the printNum function is called, passing the actual argument to void printNum, then control flows to cout which displays 1, then condition is checked, validates, num is incremented by recursive fuction, here i believe the complier (which obviously has to) keeps incrementing num by 1 and every time it does that the control goes back to cout<<num (above if condition) displaying 123456789, now after reaching 9 the condition fails, and the function recurs, when it rolls back, the control flow jumps to the statement cout<<num after the if block hence 987654321 .... I hope all are understanding me, is my perception about recursion right?? if yes then kindly explain how the same behaviour of recursive function happens with two TOH function in my first query, thanks a ton.
surfingturtle 0 Light Poster
haha guys sorry, its C++ and not C+++
Labdabeta 182 Posting Pro in Training Featured Poster
Its actually not changing num at all. Instead it creates a brand new version of num in the next function call, starting from scratch. You can picture recursive functions as infinite code like this:
void printNum(int num)
{
cout<<num;
if (num<9)
{
printNum(num+1);
}
cout<<num;
}
//is basically the same as:
void printNum(int num)
{
cout<<num;
if (num<9)
{
//this is what printNum(num+1) does:
int num2=num+1;
cout<<num2;
if (num2<9)
{
//this is what printNum(num2+1) does:
int num3=num2+1;
//etc...
}
}
cout<<num;
}
This is because each function call is isolated from the others. A decent example is a recursive fibonacci example. I assume you know the fibonacci sequence. It is defined as f(x)=f(x-1)+f(x-2) and of course f(x-1)=f((x-1))=f((x-1)-1)+f((x-1)-2), etc. So a common recursive implementation of the fibonacci sequence is:
int fibonacci(int x)
{
if (x<2)//f(1)=f(0)=1
return 1;
return fibonacci(x-1)+fibonacci(x-2);
}
In this example the execution for fibonacci(3) is:
fibonacci(3){
if (3<2)
return 1;//nope
return fibonacci(3-1)+fibonacci(3-2);
}
//now we have called fibonacci(3-1) = fibonacci(2) so we have to find out what that is:
fibonacci(2){
if (2<2)
return 1;//still nope :C
return fibonacci(2-1)+fibonacci(2-2);
}
//now we have called fibonacci(2-1) = fibonacci(1) so we have to find out what that is:
fibonacci(1){
if (1<2)
return 1;//yay!
//we never get here anyways!
}
//so fibonacci(1)=1, so fibonacci(2)=1+fibonacci(2-2)
//now we have called fibonacci(2-2) = fibonacci(0) so we have to find out what that is:
fibonacci(0){
if (0<2)
return 1;//yay still
//again, we dont care about what is here
}
//so fibonacci(0)=1, and fibonacci(2)=1+1=2, so fibonacci(3)=2+fibonacci(3-2)
//now we have called fibonacci(3-2) = fibonacci(1) which we know is 1
//this fibonacci(3)=2+1=3!
When you call a recursive function control flow in your function stops and waits for the recursive call to complete! So you have to imagine infinite copies of your recursive function to be able to analyze the control flow.
surfingturtle 0 Light Poster
thanks...the fibonacci program and the "num" never changes info was of help, so the compiler creates a seperate set of variables in each call and returns back to them with values from next called recursive function, the cout<<num; statement after the if condition in PrintNum program outputs the value each time during the roll back of function to previous num values....
Sir it would be very kind of you if you explained the control flow of TOH program similar to fibonacci, I desire and need to learn it with just 3 disks.....I know it would incomprehensible and of little/no sense to decipher recursive function with larger values, but I need to know how the parameters (arguments) in tower1 tower2 tower3 changes sequentially each time in the two cout statements considering only 3 disks, practically it was too easy to figure out, but how the program shuffles them is intriguing and beautiful, more interesting part is dissolving the problem into subproblems [step1 (n-1), step2single move, step3(n-1)] is genius, hope you would do the needful, it would be of great help. Thanks.
Labdabeta 182 Posting Pro in Training Featured Poster
Okay, here goes:
// A | B | C
TOH(3,A,B,C)// 123| |
{
if (3==1)
{//it doesn't matter what's in here anyways
}
TOH(3-1,A,C,B);//note that B,C got switched
//the above actually moves 3-1=2 disks from A to C
// A | B | C
// 3 | | 12
//we will look at how it does this next
move from A->B;// | 3 | 12
TOH(3-1,C,B,A);//note that A,C got switched
//the above actually moves 3-1=2 disks from C to B
// A | B | C
// |123|
//ta-da!
}
//now we need to look at TOH(2,A,C,B) [line 7]
// A | C | B <-- note the new order!
TOH(2,A,C,B)// 12| |
{
if (2==1)
{//it doesnt matter
}
TOH(2-1,A,B,C);//note that C,B got switched
//the above actually moves 2-1=1 disk from A to B
// A | C | B
// 2 | | 1
//We will also look at this later
move from A->C; | 2 | 1
TOH(2-1,B,C,A);//note that order is reversed
//the above actually moves 2-1=1 disk from B to C
// A | C | B
// | 21|
//ta-da!
}
//now we also need to look at TOH(2,C,B,A) [line 13]
//however it should be clear that it will work exactly like the ones above
//so we can be pretty sure that it WILL correctly move 2 disks from C to B
//finally lets look at TOH(1,A,B,C) [line 26]
TOH(1,A,B,C)//<---Read: Move 1 disk from A to B
{
if (1==1)
{
move from A->B;//yay!
return;//so we dont keep going!
}
//again, don't care!
}
Its almost easier to understand if we make our function a bit differently. Here is an easier to understand version of your code:
void Move(int howMany, char fromTower, char toTower, char extraTower)
{
if (howMany==1)
{
cout<<"Move 1 disk from "<<fromTower<<" to "<<toTower<<endl;
return;
}
Move(howMany-1,/*from*/fromTower,/*to*/extraTower,/*extra=*/toTower);
cout<<"Move 1 disk from "<<fromTower<<" to "<<toTower<<endl;
Move(howMany-1,/*from*/extraTower,/*to*/toTower,/*extra=*/fromTower);
}
By assuming that it works this is actually fairly clear:
Moving 1 disk is trivial, you just move it.
To move more than 1 disk you first move all the small ones to your extra tower, then you move your biggest disk to the final tower, then you move all the small disks on top of it.
Here is a small MSPaint drawing of that:
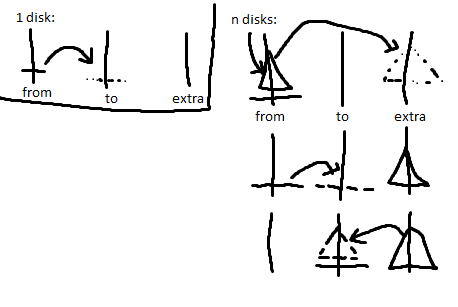
surfingturtle 0 Light Poster
everytime the void TOH (parent) function is recursively called by the both TOH function inside it, its parameters are altered accordingly which in turn modifies the parameters in both TOH (child) functions, guess thats how the parameters are been switched till d becomes 1 and the cout function is invoked, thereby displaying the move of disks....
I realized my mistake in the control flow I charted out, the whole of void TOH function is called recursively obviously containing both the child functions, instead of thinking the child function calling itself again and again, silly me .....
Thanks labdabeta ........ :'( (thats tears of joy)
Be a part of the DaniWeb community
We're a friendly, industry-focused community of developers, IT pros, digital marketers, and technology enthusiasts meeting, networking, learning, and sharing knowledge.
