Member Avatar for rhoit

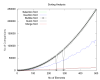
I was trying to Compare the 5 Sorting Algorithms using 4 test cases.

Sorting Algorithms

  1. Selection Sort
  2. Insertion Sort
  3. Bubble Sort
  4. Quick Sort
  5. Merge Sort

Test cases

  1. Random Data (completed)
  2. Reverse Sorted Data (completed)
  3. Almost Sorted Data (can't generate Data)
  4. Highly Repetitive Data (can't generate Data)

At first I chose C++ which went to disaster and i finally end up using Octave.
I successfully tested for Random and Reverse Sorted Data .

But in other 2 Couldn't even generate data.....

the what i have done so far have been attached with the post....
i have rename *.m file to *.txt in attachment

Sort.Analysisplot1_.png 31.2 KB 
%Title: Sort Analysis
%Objective: Insertion, Bubble, Selection, Quick, Merge Sort Analysis
%Date: 2010 Feb 5
%Author: Rhohitman (rhohitman@gmail.com)
%Description: NA

clear all;

function cntcmp=InsertionSort(A, n, N)
	cntcmp=0;
	for j=n+1:N
		cntcmp=cntcmp+1; %for
		key=A(j);
		i=j-1;		
		while( (i>=n) && (key<A(i)) )			
			cntcmp=cntcmp+2; %while
			A(i+1)=A(i);
			i=i-1;
		endwhile
		A(i+1)=key;
	endfor
endfunction

function cntcmp=BubbleSort(A, n, N)
	cntcmp=0;
	for i=n:N-1
		cntcmp=cntcmp+1; %for
		skip=0;
		for j=i+1:N
			cntcmp=cntcmp+1; %for
			cntcmp=cntcmp+1; %if
        		if(A(i) > A(j))	       				
        	        skip++;
	        		swap=A(i);
		        	A(i)=A(j);
        			A(j)=swap;
			endif
		endfor
		cntcmp=cntcmp+1; %if
		if (skip == 0) break; endif
	endfor
endfunction

function cntcmp=SelectionSort(A, n, N)
	cntcmp=0;
	for i=n:N-1
		cntcmp=cntcmp+1; %for
		for j=i+1:N
			cntcmp=cntcmp+1; %for
			cntcmp=cntcmp+1; %if
			if(A(i)>A(j))
				swap=A(i); A(i)=A(j); A(j)=swap;
			endif
		endfor
	endfor
endfunction

function QuickSort(n, N)
	global Ag;
	global gcount;
	
	gcount++; %if
	if(n<N)
		%Partition
		x=Ag(N);
		p=n-1;

		for j=n:N-1
			gcount++; %for
			gcount++; %if
			if(Ag(j)<=x)				
				p++;
				swap=Ag(p); Ag(p)=Ag(j); Ag(j)=swap;
			endif
		endfor
		
		p++;
		swap=Ag(p); Ag(p)=Ag(N); Ag(N)=swap;
		
		QuickSort(n, p-1);
		QuickSort(p+1, N);		
	endif
endfunction

function MergeSort(n, N)
	global Ag;
	global gcount;
	gcount++; %for
	if(n<N)
		p= floor((n+N)/2);
		
		MergeSort(n, p);
		MergeSort(p+1, N);
        
		i=n;
		k=n;
   		j=p+1;
   		
		while((i<=p)&&(j<=N)) gcount+=2; %while
			gcount++; %if
			if(Ag(i)<Ag(j)) B(k++)=Ag(i++);
			else B(k++)=Ag(j++);
			endif
		endwhile
		while(i<=p) gcount++; B(k++)=Ag(i++); endwhile
	   	while(j<=N) gcount++; B(k++)=Ag(j++); endwhile
		
		for k=n:N; Ag(k)=B(k); endfor
	endif	
endfunction

sample=5;

l=1; %lower limit
L=20; %upper limit
npp=5;

n=l;
k=1;

global Ag;
global gcount;
while (n<=L)
	B=round(rand(1,n)*100);

	%Sorting Random
	rand_cntcmp_ins(k)=InsertionSort(B, 1, n);
	rand_cntcmp_bub(k)=BubbleSort(B, 1, n);
	rand_cntcmp_sel(k)=SelectionSort(B, 1, n);
	
	Ag=B; gcount=0;
	QuickSort(1, n);
	rand_cntcmp_qui(k)=gcount;

	Ag=B; gcount=0;
	MergeSort(1, n);
	rand_cntcmp_mer(k)=gcount;

	%Sorting Reverse Sorted
	B=fliplr (Ag);
	rev_cntcmp_ins(k)=InsertionSort(B, 1, n);
	rev_cntcmp_bub(k)=BubbleSort(B, 1, n);
	rev_cntcmp_sel(k)=SelectionSort(B, 1, n);
	
	Ag=B; gcount=0;
	QuickSort(1, n);
	rev_cntcmp_qui(k)=gcount;

	Ag=B; gcount=0;
	MergeSort(1, n);
	rev_cntcmp_mer(k)=gcount;
		
	n=n+npp;
	k++;
endwhile

hold off;
subplot(2,2,1)
plot(l:npp:L,rand_cntcmp_sel, 'g');
hold on;
plot(l:npp:L,rand_cntcmp_ins);
plot(l:npp:L,rand_cntcmp_bub, '-xk');
plot(l:npp:L,rand_cntcmp_qui,'-p');
plot(l:npp:L,rand_cntcmp_mer,'r');

xlabel('No of Elements');
ylabel('No of Comparisions');
title('Sorting Analysis: Random Numbers');
legend('Selection Sort', 'Insertion Sort', 'Bubble Sort', 'Quick Sort', 'Merge Sort', 'location', 'northwest');

hold off;
subplot(2,2,2)
plot(l:npp:L,rev_cntcmp_sel, 'g');
hold on;
plot(l:npp:L,rev_cntcmp_ins);
plot(l:npp:L,rev_cntcmp_bub, '-xk');
plot(l:npp:L,rev_cntcmp_qui,'-p');
plot(l:npp:L,rev_cntcmp_mer,'r');

xlabel('No of Elements');
ylabel('No of Comparisions');
title('Sorting Analysis: Revese Sorted Numbers');
legend('Selection Sort', 'Insertion Sort', 'Bubble Sort', 'Quick Sort', 'Merge Sort', 'location', 'northwest');
  • 1 Contributor
  • 1 Reply
  • 866 Views
  • 1 Day Discussion Span
  • Latest Post Latest Post by rhoit
Member Avatar for rhoit

I successfully tested for all the test cases
Test cases

  1. Random Data (completed)
  2. Reverse Sorted Data (completed)
  3. Almost Sorted Data (completed)
  4. Highly Repetitive Data (completed)

But Its taking almost too much time...
for n=1 to 200 with increment of 10 it almost took 2 min...

It crossed the max recursion doing till 500 ... :(
Any Idea how to speed up & improve for more than N=5000.

i have attached the new file and graph with the post.

Screenshot-Untitled_Window.png 26.02 KB 
%Title: Sort Analysis
%Objective: Insertion, Bubble, Selection, Quick, Merge Sort Analysis
%Date: 2010 Feb 5
%Author: Rhohitman (rhohitman@gmail.com)
%Description: NA

clear all;

function cntcmp=InsertionSort(A, n, N)
	cntcmp=0;
	for j=n+1:N
		cntcmp++; %for
		key=A(j);
		i=j-1;		
		while( (i>=n) && (key<A(i)) )			
			cntcmp+=2; %while
			A(i+1)=A(i);
			i--;
		endwhile
		A(i+1)=key;
	endfor
endfunction

function cntcmp=BubbleSort(A, n, N)
	cntcmp=0;
	for i=n:N-1
		cntcmp++; %for
		skip=0;
		for j=i+1:N
			cntcmp+=2; %for & if
        		if(A(i) > A(j))	       				
        	        skip++;
	        		swap=A(i);
		        	A(i)=A(j);
        			A(j)=swap;
			endif
		endfor
		cntcmp++; %if
		if (skip == 0) break; endif
	endfor
endfunction

function cntcmp=SelectionSort(A, n, N)
	cntcmp=0;
	for i=n:N-1
		cntcmp++; %for
		for j=i+1:N
			cntcmp+=2; %for & if
			if(A(i)>A(j))
				swap=A(i); A(i)=A(j); A(j)=swap;
			endif
		endfor
	endfor
endfunction

function QuickSort(n, N)
	global Ag;
	global gcount;
	
	gcount++; %if
	if(n<N)
		%Partition
		x=Ag(N);
		p=n-1;

		for j=n:N-1
			gcount++; %for
			gcount++; %if
			if(Ag(j)<=x)				
				p++;
				swap=Ag(p); Ag(p)=Ag(j); Ag(j)=swap;
			endif
		endfor
		
		p++;
		swap=Ag(p); Ag(p)=Ag(N); Ag(N)=swap;
		
		QuickSort(n, p-1);
		QuickSort(p+1, N);		
	endif
endfunction

function MergeSort(n, N)
	global Ag;
	global gcount;
	gcount++; %for
	if(n<N)
		p= floor((n+N)/2);
		
		MergeSort(n, p);
		MergeSort(p+1, N);
        
		i=n;
		k=n;
   		j=p+1;
   		
		while((i<=p)&&(j<=N)) gcount+=2; %while
			gcount++; %if
			if(Ag(i)<Ag(j)) B(k++)=Ag(i++);
			else B(k++)=Ag(j++);
			endif
		endwhile
		while(i<=p) gcount++; B(k++)=Ag(i++); endwhile
	   	while(j<=N) gcount++; B(k++)=Ag(j++); endwhile
		
		for k=n:N; Ag(k)=B(k); endfor
	endif	
endfunction

sample=5;

l=1; %lower limit
L=200; %upper limit
npp=10;

n=l;
k=1;
range=[ 1 L*L ];
global Ag;
global gcount;
while (n<=L)
	B=round(range(1)+(range(2)-range(1)).*rand(1,n));

	%Sorting Random
	rand_cntcmp_ins(k)=InsertionSort(B, 1, n);
	rand_cntcmp_bub(k)=BubbleSort(B, 1, n);
	rand_cntcmp_sel(k)=SelectionSort(B, 1, n);
	
	Ag=B; gcount=0;
	QuickSort(1, n);
	rand_cntcmp_qui(k)=gcount;

	Ag=B; gcount=0;
	MergeSort(1, n);
	rand_cntcmp_mer(k)=gcount;

	%Sorting Reverse Sorted
	B=fliplr (Ag);
	rev_cntcmp_ins(k)=InsertionSort(B, 1, n);
	rev_cntcmp_bub(k)=BubbleSort(B, 1, n);
	rev_cntcmp_sel(k)=SelectionSort(B, 1, n);
	
	Ag=B; gcount=0;
	QuickSort(1, n);
	rev_cntcmp_qui(k)=gcount;

	Ag=B; gcount=0;
	MergeSort(1, n);
	rev_cntcmp_mer(k)=gcount;
		
	%Sorting Almost Sorted
	B=Ag;
    	
    	dis_n=ceil(.1*n); %randomizing 10% of the element again form sorted list
	dis_pos=ceil(1+(n-1).*rand(1,dis_n));
	
	for dp=1:dis_n
        	p=dis_pos(dp);
		B(p)=round(rand()*1000);
	endfor        
    
	almo_cntcmp_ins(k)=InsertionSort(B, 1, n);
	almo_cntcmp_bub(k)=BubbleSort(B, 1, n);
	almo_cntcmp_sel(k)=SelectionSort(B, 1, n);
	
	Ag=B; gcount=0;
	QuickSort(1, n);
	almo_cntcmp_qui(k)=gcount;

	Ag=B; gcount=0;
	MergeSort(1, n);
	almo_cntcmp_mer(k)=gcount;	

	%Sorting Highly Repetavie Random	
	B=round(1+(n/3-1).*rand(1,n));
	
	rep_cntcmp_ins(k)=InsertionSort(B, 1, n);
	rep_cntcmp_bub(k)=BubbleSort(B, 1, n);
	rep_cntcmp_sel(k)=SelectionSort(B, 1, n);
	
	Ag=B; gcount=0;
	QuickSort(1, n);
	rep_cntcmp_qui(k)=gcount;

	Ag=B; gcount=0;
	MergeSort(1, n);
	rep_cntcmp_mer(k)=gcount;
    
	if(n==1) n=0; l=0; endif
	n+=npp;
	k++;
endwhile

hold off;
subplot(2,2,1)
plot(l:npp:L,rand_cntcmp_sel, 'g');
hold on;
plot(l:npp:L,rand_cntcmp_ins);
plot(l:npp:L,rand_cntcmp_bub, '-xk');
plot(l:npp:L,rand_cntcmp_qui,'-p');
plot(l:npp:L,rand_cntcmp_mer,'r');

xlabel('No of Elements');
ylabel('No of Comparisions');
title('Sorting Analysis: Random Numbers');
legend('Selection Sort', 'Insertion Sort', 'Bubble Sort', 'Quick Sort', 'Merge Sort', 'location', 'northwest');

hold off;
subplot(2,2,2)
plot(l:npp:L,rev_cntcmp_sel, 'g');
hold on;
plot(l:npp:L,rev_cntcmp_ins);
plot(l:npp:L,rev_cntcmp_bub, '-xk');
plot(l:npp:L,rev_cntcmp_qui,'-p');
plot(l:npp:L,rev_cntcmp_mer,'r');

xlabel('No of Elements');
ylabel('No of Comparisions');
title('Sorting Analysis: Revese Sorted Numbers');
legend('Selection Sort', 'Insertion Sort', 'Bubble Sort', 'Quick Sort', 'Merge Sort', 'location', 'northwest');

hold off;
subplot(2,2,3)
plot(l:npp:L,almo_cntcmp_sel, 'g');
hold on;
plot(l:npp:L,almo_cntcmp_ins);
plot(l:npp:L,almo_cntcmp_bub, '-xk');
plot(l:npp:L,almo_cntcmp_qui,'-p');
plot(l:npp:L,almo_cntcmp_mer,'r');

xlabel('No of Elements');
ylabel('No of Comparisions');
title('Sorting Analysis: Almost Sorted Numbers');
legend('Selection Sort', 'Insertion Sort', 'Bubble Sort', 'Quick Sort', 'Merge Sort', 'location', 'northwest');

hold off;
subplot(2,2,4)
plot(l:npp:L,rep_cntcmp_sel, 'g');
hold on;
plot(l:npp:L,rep_cntcmp_ins);
plot(l:npp:L,rep_cntcmp_bub, '-xk');
plot(l:npp:L,rep_cntcmp_qui,'-p');
plot(l:npp:L,rep_cntcmp_mer,'r');

xlabel('No of Elements');
ylabel('No of Comparisions');
title('Sorting Analysis: Highly Repetative Numbers');
legend('Selection Sort', 'Insertion Sort', 'Bubble Sort', 'Quick Sort', 'Merge Sort', 'location', 'northwest');
Edited by rhoit because: n/a
Be a part of the DaniWeb community

We're a friendly, industry-focused community of developers, IT pros, digital marketers, and technology enthusiasts meeting, networking, learning, and sharing knowledge.