how to build an expression tree from string.

[vs88]

Hi.
i need to build an expression tree from a string and i dont get how to do it.

for exapmle:

str[20]="( (2 + 5) * (8 / 2))";

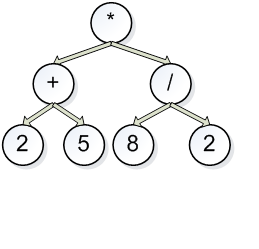
can some one help me?

thanks.

[Schol-R-LEA]

Essentially, this is an issue of parsing, though one with a fairly limited scope. The usual solution is to build a stack (explictly or implicitly) to represent the order of operations in postfix form. You could then convert said stack to a tree structure quite easily.

I would recommend doing a series of searches about 'expression parsing', 'infix to postfix conversion', and related terms, both on this website and through a web search engine. There should be a wealth of information around, though you may need to look at it critically as there's a wealth of misinformation around as well.

I know this doesn't really answer the question directly, but it should give you a direction to look in. We cannot give out wholesale answers here - and it would be counter-productive for both you and us if we did - but we will advise you as best we can.

[vs88]

It can be another way without a stuck?

I tried to write something, I know it's not entirely true, maybe you can help me fix this?

I have a way to fix it?

this what i write.

TreeNode * BuildTree(char * str,unsigned int  *n) //in the begining n=0;
{
    TreeNode * left, *right, *tr;


    tr = left = right = NULL;

    if (str[0] == '\0')
        return NULL;
    else
    {
        if (str[0] >= '0' && str[0] <= '9')
            tr = AlocateTreeNode(str[0]); //creat a new leaf.
        else
            if (str[0] == '(')
            {

            left = BuildTree(str + 1, n);


            tr = AlocateTreeNode(str[2 + 4 * (*n)]);
            right = BuildTree(str + 3 + 4 * (*n), n);



            *n = *n + 1;

            tr->left = left;
            tr->right = right;

            }



        return tr;
    }

[Schol-R-LEA]

You don't need an explict stack if you are building the tree recursively, no; the implicit stack created by the recursive calls will do the job quite nicely.

However, there are definite problems with the way you are handling the string processing. You are using explicit indexing of the string at fixed offsets, which will prove problematic if you need to a) read in a numeric value of more than one digit, and b) have more than one nested sub-expression. For example, if you code expects a single digit for a value node, then this line will fail if given more than one digit:

tr = AlocateTreeNode(str[0]);

It will also fail if given a simple (non-parethesized) expression such as "2 + 2", as it assumes that any value that isn't in parentheses is a single value.

More importantly, if there is an expression nested inside of a parenthesized expression, such as "((2 - 1) * (4 + 3))", then this line will also fail:

tr = AlocateTreeNode(str[2 + 4 * (*n)]);

In any case, the index isn't getting updated in the calling functions following a recursive call, so it will keep reading the same part of the string over and over again.

The best solution to this, IMAO, is to write string-reading function, which handles to index for you by keeping a static local index (or, if you find a need for pushback - which you might - a global index shared by two functions), and a minimal tokenizing function, which would call the string-reading function a character at a time and build up the values (tokens). This in turn would be called by BuildTree() to get the components of the AST (abstract syntax tree). This moves the concerns of both string handling and token recognition out of BuildTree() which can then work on interpreting the expression syntax without having to juggle the string indices or worry about the size of the numbers.

I would recommend a simple struct that holds both the token type (in this case, either an integer, an operator, or a parenthesis) and a token value (a string of suitable length, say, 33 characters - 32 plus maximum delimiter).

enum TOKEN_TYPE {ERR, INT, OP, PAREN};

struct Token
{
    TOKEN_TYPE type;
    char value[MAX_VAL];
};

The lexical analyzer would be fairly simple: at the start of each new token, it would read in characters until it finds one that is not a whitespace character. The it would have a switch to determine if the first usable character of the new token is an digit (using isdigit()), and if it is, it should keep reading in digits until it finds a non-digit, which it would push back (that is to say, it would decrement the index by one), then store the value and the INT type in the Token to be returned. For a paren or an operator (assuming just the typical one-character ops - if you want two-character operators, you'll do the same thing as with numbers), it would just return a Token with the appropriate value and type. Any values that aren't any of those would return an ERR with the offending character as the value.

Since you'll probably need to do all of this eventually (given the logical assumption that this is the first or second assignment in a compiler course - it typically is), it's better to get a head-start on doing it this way, anyway.