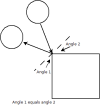
I was wondering what would be the best way to implement an algorythm to figure out what side a circle has collided with a rectangle?
After check to make sure a circle has collided with the rectangle im trying to figure out how to know what side of the rectangle was hit. The problem is the rectangle is smaller than the circle somtimes.... everything ive tried so far will only work if the rectangle is bigger than the circle..
Any ideas will be greatly appreciated.
Scheppy.
Think more in terms of "intersecting", "overlapping", and "touching" rather than "colliding". Similar concepts but the math is easier if you think in terms of two shapes' PRESENT states (the terms I've used) as opposed to "colliding", which requires more thinking in terms of PAST states and motion. Make it as simple as possible.
I'm going to use "touching" and "overlapping" and "intersecting" loosely here, roughly as synonyms. It's easy to change things up a little to make them distinct and tailored to your particular problem. The definition distinctions may or may not be important. Think conceptually. A rectangle intersects a circle if any of its four sides intersect the circle. Each side is a line segment. You have three possible distances to check to determine this. The first two are easy. Calculate the distances between the circle's center and each of the two line segment endpoints. If that distance is less than the circle's radius, they intersect. If it's exactly equal, they touch and may intersect. Recall you are dealing with doubles and rounding off. My view is just go with "less than or equal" and don't worry about touching versus intersecting.
If both distances are GREATER than the circle's radius, you have one more distance to check. Extend the line segment into a line. Draw a line segment from the circle's center to that line so that it is perpendicular to the line. Determine whether that line segment touches the original line segment that is part of the rectangle side. If it is, determine the length of that line segment. If it is less than or equal to the circle's radius, the rectangle and the circle intersect on that side of the rectangle.
Hopefully this makes sense. This all assumes that the rectangles are potentially at an angle. If they are strictly horizontal/vertical, the math is easier.
So... pencil and paper time. Dust off the Geometry book. If the above description doesn't make sense after that, lemme know and I'll try to draw you a picture.
You can check for the two Shapes (ellipse and rectangle) intersecting. Which side is then just a tedious testing of the x and y coordinates.
Bouncing off a side of a rectangle (assuming it;s horiontal/vertical) is trivial (1), but bouncing off a corner is a different question. If you get a decent solution then please share it.
(1) if circle.centre.y < top of rectangle && > bottom of rectangle and dx > 0 then it was the left side. Etc
ok guys, I will let you know what I come up with. and yes my rectangles will somtimes be rotated...
@ AssertNull thanks for the tips. I was hoping thier was going to be an easy way to go about this.
@james. Yes i will be checking first if the rectangles intercect...
Than i will be checking if the circle is accually touching/overlapping the rectangle,
and than maybe combines with if the circle is touching find out what side is touching.
I will let you guys know.
I was hoping thier was going to be an easy way to go about this.
"Easy" is relative. As I think I mentioned, if the rectangle is vertical/horizontal as opposed to at an angle, it is considerably easier. But still not trivial.
Regarding bouncing off a corner, I think a semi-easy way is to treat it as if there was an imaginary wall balancing on the point with equal angles from the adjacent edges (see attached image).
The more I think about it, the more I like James' idea of letting Java do a lot of the math work as far as figuring out whether things intersect. In Java, as in math, a Rectangle is a Polygon, which is simply a closed Shape made up of line segments, in your case 4. If your rectangles are allowed to tilt, you can't use Rectangle (note the capitalization and lower-case here. Upper case is a class name) unless you use AffineTransforms to tilt things I believe. Not worth it IMO. If you are going to tilt things, use Polygon, which is a 4 sided closed Shape with right angles and line segments as the edges. Here's what you do. Keep track of the 4 corners. From those 4 corners, create your Polygon. Polygon and Ellipse are both Shapes, so use the Ellipse.intersects(Shape) function to determine collisions. For the details about whether it has collided with each of the four corners, use Ellipse.contains(Point). Now for the edges. You probably can't use the contains function because a Line has no area. BUT you can create an incredibly thin Rectangle or Polygon from the two Points that make up the edge, so if your edge is from, say (0,0) to (2,3), create a Polygon with Points (0,0) to (0,0.00001) to (2,3.00001) to (2,3) and back to (0,0). Now check the Ellipse.intersects(Polygon) function to see if the circle has collided with that edge.
Java does most of the math.
Yes, don’t reinvent the wheel.
Re bouncing off sides:
In practice you do need to consider the direction of motion (a) because that's simpler and (b) otherwize you get artifacts from the non-continuous simulation (ball overlaps rect at tick n, you reverse direction, but at tick n+1 it may not yet have cleared the rect but you don't want to treat that as another bounce).
Re bouncing off a corner - the imaginary wall needs to be normal to the line joining the corner to the circle's center I believe.
If you already have working code for 2 balls bouncing off each other then you can replace the corner by a very small very heavy ball and use the existing code.
All very good points, Thanks guys.
Still working on it :)
I'm going to reverse myself once again. Or perhaps remain agnostic. I was looking at the Java 8 Shape API. What I thought would be there and isn't as far as I can tell is something like this, in Shape...
boolean intersects(Shape s)It has this...
boolean intersects(Rectangle2D r)All fine and good until we recall that the OP has to deal with rectangles which are tilted. Again, unless we do some clever AffineTransforms somewhere, I'm thinking that Java does not provide this, at least Oracle's main release doesn't. I have to believe that there's a solid reliable well-tested publicly released third party Java library that provides the answer (it comes up so often there has to be), but again, I don't see it as part of the main official release.
Barring that, again, see my earlier posts and dust off some good Geometry and Trigonometry and Physics books because you may be writing some of the math yourself. I'd be interested in James' take on this. I am surprised that Oracle doesn't at least have a Polygon2D.Double and an Ellipse.intersects(Polygon) function even if they've decide not to do a more general Shape.intersects(Shape) function. Again, with the caveat that I may have missed something obvious.
Have a look at java.awt.geom.Area - it implements Shape but represents a closed shape at a particular position. It has all kinds of useful methods that Shape doesn't have, including area.intersects(other area)
Here's code I used a while back to do an exact check on collision between two arbitrary Shapes. It gets the Area from each shape, translates them to the correct x.y position, and intersects them. If the intersection is empty then they do not overlap.
private boolean exactCollision(Sprite s1, Sprite s2) {
Area a1 = new Area(s1.getShape());
a1.transform(AffineTransform.getTranslateInstance(s1.getX(), s1.getY()));
Area a2 = new Area(s2.getShape());
a2.transform(AffineTransform.getTranslateInstance(s2.getX(), s2.getY()));
a1.intersect(a2);
return !a1.isEmpty();
}James still working on my thing,
but it find that very interesting so i just tested it out. like so
//checking if a ball has hit the bonus
for (int x = 0; x < CircleRect.size(); x++) { if(exactCollision(CircleRect.get(x),Ballgame.Bonus.getBonusRect())){
System.out.println("Collision Detected");
Ballgame.ballGame.setRunning(false);
}
}and this
private boolean exactCollision(Rectangle RectA, Rectangle RecB) {
Area a1 = new Area(RectA.getBounds());
a1.transform(AffineTransform.getTranslateInstance(RectA.getX(), RectA.getY()));
Area a2 = new Area(RecB.getBounds());
a2.transform(AffineTransform.getTranslateInstance(RecB.getX(), RecB.getY()));
a1.intersect(a2);
return !a1.isEmpty();
}So im not sure but RectA is the rectangle with the circle in it... and rectangle b is just a normal small rectangle...
It detects the collision... but it is extremly inaccurate.
I can see where it detects the collision because it pauses the gameloop...
somtimes the circle is halfway into the rectangle already and somtimes just touching... other times it doesant even detect if if a circle grazes it or comes by halfway overlapping the rectangle? What would this method be used for??
Looks like you're combining a few different concepts. Hard to say without the full code, but it SEEMS like you are comparing whether the BOUNDING rectangle of the circle intersects the other rectangle. In other words, your checking whether two rectangles intersect when you need to check whether a circle and a rectangle intersect.
My advice would be to forget about tilted rectangles for a while. And forget about AffineTransforms and Areas and Sprites (if you are even using them now). Create an Ellipse (a circle in your case) and a Rectangle and see if you can detect collisions PERFECTLY using the plain old Rectangle and Ellipse classes and their derivatives (Ellipse2D.Double and Rectangle2D.Double).
The key phrase above is "for a while". You can go back to them and get more complex when you get the hang of the Ellipse2D.Double and Rectangle2D.Double and their intersections. Thus, I'm not disagreeing with James' code and advice, just saying use it in good time after you master the above. A "crawl before you walk" thing because I think you are confused and comparing two rectangles, which is going to give you bad results. Good luck.
ok, so would this would also be done for painting...? i know about the circles.. its just i wouldent know how to paint them.... only inside a rectangle... or would i convert my rectangle with a circle painted inside of it (im using "fill oval")to a circle for calculations only??
Yes I guess i am a little confused.
Rectangle2D and Ellipse2D imports are from Java 8's java.awt.geom package.
// change these values to experiment
double circleDiameter = 100;
double circleUpperLeftx = 50;
double circlUpperLefty = 50;
double rectangleLength = 100;
double rectangleWidth = 100;
double rectangleUpperLeftx = 200;
double rectangleUpperLefty = 200;
Rectangle2D.Double rectangle = new Rectangle2D.Double(rectangleUpperLeftx, rectangleUpperLefty, rectangleWidth, rectangleHeight);
Ellipse2D.Double circle = new Ellipse2D.Double(circleUpperLeftx, circleUpperLefty, circleDiameter, circleDiameter);Assuming you are painting them using a Graphics2D object called g2, the following code will paint them solid if they do not intersect and hollow if they do...
if(circle.intersects(rectangle))
{
g2.draw(circle);
g2.draw(rectangle);
}
else
{
g2.fill(circle);
g2.fill(rectangle);
}wow perfect. ok since its 12:40 am here i will go to bed. but this gives me plenty to do tomorrow evening. Thank you very much. I will be testing this and than changing a bunch of my currant setup.
this accually just gave me a huge knowledge boost. everything just came together. !!
Thanks!
What would this method be used for?
It tests for two Shapes overlapping. They can be rectanges, circles, polygons or completely arbitrary Shapes. If you have a Circle then that's the shape you should be using, not its bounding rectangle.
in the program I took that code from the moving objects ("Sprites") are actually transparent GIF Images. The Shape is a compound thing I hand-craft to fit reasonably round the visible part of the image so I can detect collisions between the visible parts of two Images.
I agree with AN's advice to get something simple working first before moving on to harder stuff. BUT you should accept that the simple stuff is just a learning exercise and not the base for a final implementation. Before you ge too far you have to take what you have learned, set aside the learning code, and think through a proper design for the real thing. Just adding complexity to an arbitrary simple case is a formula for chaos!
Ok guys, Im not going to mark this as solved just quite yet...
But You might not hear anything for a while few days or so while I play with
Java 8's java.awt.geom package. and than when all is said and done, to implement it in my code for collision.
what am I missing here.
I dont have the .draw() or .fill() here.
Using netbeans.
i only have the g2.drawRect & g2.fillRect.
This works... but i have to cast everything from double to int... which is not right because all of the examples that im seen so far this is not neccasary.
And yes Im using jave 1.8
Im missing somthing very stupid and dumb here.
First, a couple of small typos in my last post. Should be fairly obvious, but I'll correct it here.
// change these values to experiment
double circleDiameter = 100;
double circleUpperLeftx = 50;
double circleUpperLefty = 50;
double rectangleHeight = 100;
double rectangleWidth = 100;
double rectangleUpperLeftx = 200;
double rectangleUpperLefty = 200;
Rectangle2D.Double rectangle = new Rectangle2D.Double(rectangleUpperLeftx, rectangleUpperLefty, rectangleWidth, rectangleHeight);
Ellipse2D.Double circle = new Ellipse2D.Double(circleUpperLeftx, circleUpperLefty, circleDiameter, circleDiameter);Now, if you are using NetBeans, the nice thing about NetBeans is that you can type an object and it gives you some options to choose from as an auto-complete type of thing. So if you type in "g2.", a few options should come up...
Two of them are as follows...
g2.draw(Shape s)
g2.fill(Shape s)They are hollow and solid options drawing Shapes. You'll replace "Shape s" with "circle" or "rectangle", as in my code, the same names I gave them. You will, of course, need to make sure those variables are accessible in the lines above. Variety of ways to do that. I've been playing around with some samples to post here and I've decided that the best way is to copy/paste the whole class so there's no ambiguity at all how to do it, so check back in several hours...
You'll also see something like this in the Graphics class (see link below) which you can also call with a Graphics2D object.
https://docs.oracle.com/javase/8/docs/api/java/awt/Graphics.html
drawOval(int x, int y, int width, int height)Ditto for fill and ditto for the rectangle. The one above is for drawing an ellipse/oval/circle. Yes, they are integers because everything is in pixels. The difference between that and
draw(Shape)
is that in your case, the Shape is going to be circle, which is an Ellipse2D, which CONTAINS the x, y, width, and height (width and height is same for circle), so there is no need to provide those arguments since the Ellipse2D object already contains them.
So, these two functions are basically the same. You can either pass it the x,y,width,length or you can pass it an Ellipse2D containing that information.
Gotta go. Check back in several hours.
The great thing about Shape is the Ellipses, Rectangles etc are all Shapes, so the only draw method you need is draw(Shape). So leverage the classes that Java gives you and define all your movable things ("Sprites" is the jargon) as being or having a Shape and they can all share (inherit) the same simple drawing method.
Okay, give this code a try. It sort of sums up all of my points in this thread and the last one regarding collisions of the larger shapes plus the edges and corners. We're supposed to not give you full code on this site, BUT it seems to me that you've shown effort and it also seems that you're still going to have to put in MORE effort in order to incorporate the concepts into YOUR project. This should work as-is in NetBeans using Java 8.
import java.awt.Color;
import java.awt.Dimension;
import java.awt.Graphics;
import java.awt.Graphics2D;
import java.awt.GridLayout;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import javax.swing.*;
import java.awt.geom.*;
public class CollisionPanel extends JPanel implements ActionListener
{
Ellipse2D.Double circle;
Rectangle2D.Double rectangle;
JButton upButton, downButton, rightButton, leftButton, growButton, shrinkButton,
hideShowEdgeCollisionsButton, hideShowCornerCollisionsButton;
JFrame mainFrame;
JPanel buttonPanel;
boolean showEdgeCollisions = false;
boolean showCornerCollisions = false;
public static final int CHANGE_SIZE_INCREMENT = 5;
public static final int MOVE_INCREMENT = 5;
public static final Color BACKGROUND_COLOR = Color.YELLOW;
public static final Color CIRCLE_COLOR = Color.BLUE;
public static final Color RECTANGLE_COLOR = Color.GREEN;
public static final Color EDGE_COLLISION_COLOR = Color.RED;
public static final Color CORNER_COLLISION_COLOR = Color.BLACK;
private void CreateCircleAndRectangle()
{
// change these values to experiment
double circleDiameter = 100;
double circleUpperLeftx = 50;
double circleUpperLefty = 50;
double rectangleHeight = 100;
double rectangleWidth = 100;
double rectangleUpperLeftx = 200;
double rectangleUpperLefty = 200;
rectangle = new Rectangle2D.Double(rectangleUpperLeftx, rectangleUpperLefty, rectangleWidth, rectangleHeight);
circle = new Ellipse2D.Double(circleUpperLeftx, circleUpperLefty, circleDiameter, circleDiameter);
}
private void CreateButtonPanel()
{
buttonPanel = new JPanel();
buttonPanel.setLayout(new GridLayout(2, 4));
upButton = new JButton("Circle Up");
upButton.addActionListener(this);
buttonPanel.add(upButton);
downButton = new JButton("Circle Down");
downButton.addActionListener(this);
buttonPanel.add(downButton);
rightButton = new JButton("Circle Right");
rightButton.addActionListener(this);
buttonPanel.add(rightButton);
leftButton = new JButton("Circle Left");
leftButton.addActionListener(this);
buttonPanel.add(leftButton);
growButton = new JButton("Circle Grow");
growButton.addActionListener(this);
buttonPanel.add(growButton);
shrinkButton = new JButton("Circle Shrink");
shrinkButton.addActionListener(this);
buttonPanel.add(shrinkButton);
hideShowEdgeCollisionsButton = new JButton("Hide Edge Collisions");
hideShowEdgeCollisionsButton.addActionListener(this);
buttonPanel.add(hideShowEdgeCollisionsButton);
hideShowCornerCollisionsButton = new JButton("Hide Corner Collisions");
hideShowCornerCollisionsButton.addActionListener(this);
buttonPanel.add(hideShowCornerCollisionsButton);
}
public CollisionPanel()
{
mainFrame = new JFrame();
mainFrame.setMinimumSize(new Dimension(1000, 1000));
mainFrame.setLayout(new GridLayout(2, 1));
CreateCircleAndRectangle();
CreateButtonPanel();
mainFrame.add(this);
mainFrame.add(buttonPanel);
mainFrame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
public static void main(String[] args)
{
CollisionPanel cp = new CollisionPanel();
cp.mainFrame.setVisible(true);
}
public void MoveCircle(double dx, double dy)
{
circle.x += dx;
circle.y += dy;
}
public void ChangeCircleSize(double dw) // dw stands for change in width. Since circle, dh (change height) is same as dw)
{
double dh = dw;
circle.width += dw;
circle.height += dh;
}
@Override
public void actionPerformed(ActionEvent ae)
{
Object source = ae.getSource();
if(source == leftButton) MoveCircle(-MOVE_INCREMENT, 0);
else if(source == rightButton) MoveCircle(MOVE_INCREMENT, 0);
else if(source == downButton) MoveCircle(0, MOVE_INCREMENT);
else if(source == upButton) MoveCircle(0, -MOVE_INCREMENT);
else if(source == growButton) ChangeCircleSize(CHANGE_SIZE_INCREMENT);
else if(source == shrinkButton) ChangeCircleSize(-CHANGE_SIZE_INCREMENT);
else if(source == hideShowEdgeCollisionsButton)
{
showEdgeCollisions = !showEdgeCollisions;
String buttonText = "Hide Edge Collisions";
if(showEdgeCollisions)
buttonText = "Show Edge Collisions";
hideShowEdgeCollisionsButton.setText(buttonText);
}
else if(source == hideShowCornerCollisionsButton)
{
showCornerCollisions = !showCornerCollisions;
String buttonText = "Hide Corner Collisions";
if(showCornerCollisions)
buttonText = "Show Corner Collisions";
hideShowCornerCollisionsButton.setText(buttonText);
}
repaint();
}
@Override
public void paintComponent(Graphics g)
{
super.paintComponent(g);
Graphics2D g2 = (Graphics2D) g;
setBackground(BACKGROUND_COLOR);
if(circle.intersects(rectangle))
{
g2.setColor(CIRCLE_COLOR);
g2.draw(circle);
g2.setColor(RECTANGLE_COLOR);
g2.draw(rectangle);
// now check the corners and edges for collisions if the user wants
// To do this, let's grab the points of the rectangle. We do this by getting
// PathIterator from the rectangle and iterating through it to get the
// corner points. There are 4 corners of a rectangle, but the PathIterator
// will give us an extra point which is the same as the starting point, which
// is useful for our purposes. It starts at the upper left corner and
// goes clockwise to the beginning (again, upper left corner. When it
// gets to a point it's been to before, it knows to stop. This is a slight
// oversimplification, but it's good for our purposes now...).
//
// Point 0 = upper left corner
// Point 1 = upper right corner
// Point 2 = lower right corner
// Point 3 = lower left corner
// Point 4 = upper left corner (same as point 0 where we started)
PathIterator pi = rectangle.getPathIterator(null);
Point2D.Double[] rectangleCorners = new Point2D.Double[5];
double[] coords = new double[2];
double x, y;
for(int i = 0; i < 5; i++)
{
pi.currentSegment(coords);
x = coords[0];
y = coords[1];
rectangleCorners[i] = new Point2D.Double(x, y);
pi.next();
}
// okay, we now have the rectnagle corner points. If the user wants, let's
// do some more intersection testing to try to better pinpoint what exactly
// intersected.
// First, test the corners...
if(showCornerCollisions)
{
g2.setColor(CORNER_COLLISION_COLOR);
// check each corner point with the circle.
for(int i = 0; i < 4; i++)
{
if(circle.contains(rectangleCorners[i]))
{
// this point intersects. For display purposes, let's create
// a small circle with this corner at the center and paint it.
Ellipse2D.Double corner = new Ellipse2D.Double(rectangleCorners[i].x - 5,
rectangleCorners[i].y - 5, 10, 10);
g2.fill(corner);
}
}
}
// now test the edges. Slightly harder, but not too bad.
if(showEdgeCollisions)
{
g2.setColor(EDGE_COLLISION_COLOR);
for(int i = 0; i < 4; i++)
{
// Create a closed Path2D shape with a very small area by taking the two points
// of an edge and creating a triangle with those two points as one edge, then a third point
// a miniscule distance from one of them to complete the triangle
Point2D.Double point1 = rectangleCorners[i];
Point2D.Double point2 = rectangleCorners[i+1];
Point2D.Double point3 = new Point2D.Double(point1.x + 0.0001, point1.y);
// do a little test to make sure it's not SO close to the edge to make
// the area so small as to not register.
double dx = java.lang.Math.abs(point1.x - point2.x);
double dy = java.lang.Math.abs(point1.y - point2.y);
if(dx > dy)
{
// we'll get more area if we switch it around a little bit
point3.x = point1.x;
point3.y = point1.y + 0.0001;
}
Path2D.Double edgePath = new Path2D.Double();
edgePath.moveTo(point1.x, point1.y);
edgePath.lineTo(point2.x, point2.y);
edgePath.lineTo(point3.x, point3.y);
edgePath.closePath();
if(circle.intersects(edgePath.getBounds2D()))
g2.drawLine((int)point1.x, (int)point1.y, (int)point2.x, (int)point2.y);
}
}
}
else
{
g2.setColor(CIRCLE_COLOR);
g2.fill(circle);
g2.setColor(RECTANGLE_COLOR);
g2.fill(rectangle);
}
}
}@Assertnull
Unbelieveable. Ive figured it out. Ive spent the last 3 hours trying to figure out why i dident have the draw and fill shape methods in my netbeans... figuring out my java version all that dumb stuff.. and I take your code and it does work.....
This is what it was....
from this...
super.paintComponent(g);
Graphics g2d = (Graphics2D) g;To this.
super.paintComponent(g);
Graphics2D g2d = (Graphics2D) g;Thanks so much for this...
No one else has ever seemed to have this issue...... 2 letters :/!!!
Now I have the collision working perfectly. Detects it perfect.
I just need to find the exact point at where it collided to figure out how the circle bounces off again.
This makes me happy. Thanks.
So ive gotten the exact point of impact figured out.
this is what i did... quickly... gonna do it good.
private void exactCollision(Ellipse2D.Double s1, Rectangle2D.Double s2) {
Area a1 = new Area(s1);//get the area of circle
Area a2 = new Area(s2);//get the area of rectangle
//the super usefull method here is intersect.
//Sets the shape of this Area to the intersection of its current shape and the shape of the specified Area. The resulting shape of this Area will include only areas that were contained in both this Area and also in the specified Area.
a1.intersect(a2);
Ballgame.gamePainter.setRectangle((Rectangle2D.Double) a1.getBounds2D());//getting the bounds of the intercection rectangle
Ballgame.gamePainter.repaint();
Ballgame.ballGame.setRunning(false);
}This paints a green rectangle of where the 2 are overlapping.
From here i will just take the centre coordinates... this will seem to be perfect to the human eye. Barely noticable. and from that figure out what side the rectangle was hit on.
Thanks Alot guys!!!!
Heres my exact collision location
private Point exactCollision(Ellipse2D.Double s1, Rectangle2D.Double s2) {
Area a1 = new Area(s1);
Area a2 = new Area(s2);
a1.intersect(a2);
Rectangle CollisionRect = a1.getBounds();
Point point = new Point();
point.setLocation(CollisionRect.x+(CollisionRect.width/2), CollisionRect.y+(CollisionRect.height/2));
return point;
}2 letters
Ouch! Yeah. That sucks. Sometimes you get lucky and Java will al least throw you a warning. But... not here. Easy to miss. Congratulations on your tenacity on eventually catching it. Lots of people would have given up.
This is how I have thought of finding out what side was hit?? do you guys have any input on this? better way?
This seems to work good
@James "If you get a decent solution then please share it."
private void WhatSide( Ball ball, Point collisionPoint) {
//here i am getting the distance from the collision point to each of the 4 corner points of the rectangle... to figure out
//what side was hit.
Rectangle2D.Double Rect = Ballgame.Bonus.getBonusRect();//getting the rectangle object
//getting the 4 points of the rectangles corners.
Point A, B, C, D;
A = new Point();//top left
A.setLocation(Rect.x, Rect.y);
B = new Point();//top right
B.setLocation(Rect.x + Rect.width, Rect.y);
C = new Point();//bottom left
C.setLocation(Rect.x, Rect.y + Rect.height);
D = new Point();//bottom right
D.setLocation(Rect.x + Rect.height, Rect.y + Rect.width);
double collisionA, collisionB, collisionC, collisionD;//Distance Variables from collision point to each rectange corner
collisionA = A.distance(collisionPoint);
collisionB = B.distance(collisionPoint);
collisionC = C.distance(collisionPoint);
collisionD = D.distance(collisionPoint);
//now find the nearest point...
//than find the closest distance to this points connecting vertices
if (collisionA < collisionB && collisionA < collisionC && collisionA < collisionD) {
if (collisionPoint.distance(B) < collisionPoint.distance(C)) {
System.out.println("collision at Top");
} else {
System.out.println("collision at Left");
}
} else if (collisionB < collisionA && collisionB < collisionC && collisionB < collisionD) {
if (collisionPoint.distance(A) < collisionPoint.distance(D)) {
System.out.println("collision at Top");
} else {
System.out.println("collision at Right");
}
} else if (collisionC < collisionA && collisionC < collisionB && collisionC < collisionD) {
if (collisionPoint.distance(A) < collisionPoint.distance(D)) {
System.out.println("collision at Left");
} else {
System.out.println("collision at Bottom");
}
} else {
if (collisionPoint.distance(B) < collisionPoint.distance(C)) {
System.out.println("collision at Right");
} else {
System.out.println("collision at Bottom");
}
}
}This is how I have thought of finding out what side was hit?? do you guys have any input on this? better way?
Well I posted code that worked for that, so that would be my input (or at least my simplified input. See some of my other posts in your last thread for where it gets complicated). I'm a little confused by YOUR code though. I see that there is some variable called collisionPoint passed TO the function. Seems like once you've figured that out, you're pretty much done. Just note that if you find the two closest points on a SQUARE, you've found which edge it is. That's a fact of geometry. That's NOT true for a rectangle. I don't see anything that tells me this function is for a square.
But really I'm guessing you're eventually going to need a function that determines how far a point is from a line segment or perhaps a line, so I'd write it now. Why wait? Once you have that, use it for this. The collision point should be on an edge, so the distance would be 0. Or at least extremely close to 0 to add some round off and approximation error.
My feeling is that regardless of what Java provides, somehow these projects always end up with you having to do some math, so just accept that up front.
I'm worried that none of these algorithms seems to consider the velocity of the circle.
Eg
At time t the circle overlaps the top left corner of the rectangle, which means at some time betweeen t-1 and t it made first contact.
Depending on which way it was moving it could have first contacted the top (eg moving down & left) or the left side (eg moving up & right) or the corner (eg moving down & right). AFAIK there's no possibility of .determining which it was by just considering the position at some time after first contact.
I tried to distinguish these by considering the velocity and also the position of the circle centre relative to the rectangle. The results look OK to the naked eye, but I have little confidence that this is really correct for all angles of approach.
My next idea is to try to go back and find the exact moment of first contact. At that moment there is no ambiguity and just testing for circle touches point or line is enough. We know position at time t, we have the velocity, so we know the position t-1. A quich binary search of the times between those should get the first contact to within (say) 1/10 pixel very quickly...
@ AssertNull Yup What was I thinking. This isnt going to work at all down the line.
yes James your right. lemme try to redo this one. Ill have to look up the binary search/
Hold fire... I have a better idea..
Imagine the rect. Now draw an extended shape around it that's distance r from the rect (where r is the radius of the circle). That shape has 4 straight segments and 4 ninety degree arc segments.
At the point of contact the center of the circle is on exactly one of those 4+4 segments.
Now draw the lines segment joining the position of the center of the circle at the previous time step with its position now.
If there was a collision then that line will intersect one of the 4+4 segments, and which one tells you which side/corner it collided with.
LIne2D has an intersects method that tells if two straight line segments intersect.
Line2D has a ptSegDist method that gives you the closest distance between a line segment and a point. If the point is the center of a circle and the distance is less than the radius then the segment intersects the circle. Voila! The Java API has al the geometric methods we need!
Just one possible complication: depending on the speeds and sizes and the size of the time step, the circle's center could enter and leave the extended shape in one tick. That case gives you two intersections, and you have to use the velocity to see which was the entry point. A little tedious set of if tests, but not in any way hard.
Summary: This algorithm should be exactly correct for all possible values, uses existing APIs for all the calculations, works for rectangles at an angle, and should be really fast.
I'll tr to code it later today, but please feel free to do it first!
JC
ps: ptSegDistSq gives the square of the distance from a line segment to a point. Compare it to radius squared and you avoid an expensive square root calculation.
We're a friendly, industry-focused community of developers, IT pros, digital marketers, and technology enthusiasts meeting, networking, learning, and sharing knowledge.