Finite automata to regular expression

Hello All!

Please note that this is not an assignment. I have solved the problem but I just need to know the concept behind this solution.

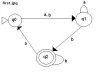
Convert FA (See first.jpg) into regular expression through TG.

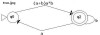
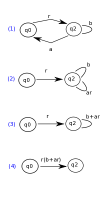
See two.jpg and three.jpg for solution.

So the required RE would be ((a+b)a*b)(b+a((a+b)a*b))*

It is all ok up to two.jpg. But I am greatly confused in three.jpg.

I don't understand the concept, how the transition "a" going from "q2" to "q0" is eliminated in last image.

Any suggestion would be greatly helpful.

Thanks!

Any computer science genius please help?

[0x69]

I'm not expert, but will try to answer. Make substitution r=(a+b)a*b (it will be easier to analyze), then you will get such picture below. So basically 'a' transition is used to make 'ar' transition. Hope that helps.

[hellojoe]

I don't understand the concept, how the transition "a" going from "q2" to "q0" is eliminated in last image.

Any suggestion would be greatly helpful.

Thanks!

It doesnt, in image three you use the regular expression from two to get to q2 then you can either loop on q2 with input b or move to state q0 with input a and then the regular expression from image two again to get back to q2

[s_sridhar]

I think it is rather self explanatory... from q0 if you apply either a or b (given by (a+b) you go to q1. Then there is a self loop from q1 on application of a. So you get that a* term. From q1 when you apply b you go to the final state q2. So... From q0 how do you go to q2?? (a+b)a*b.... From q2 there is a transition to q0 on application of a.. It is written as such.

Now we have got the diagram 2. We should simplify diagram 2 into diagram 3.. How do you go to q2 from q0?? either by the direct transition (a+b)a*b or you can also go like this... from q0 to q2 then apply a to come back to q0 and then apply (a+b)a*b or you can keep looping around q2 repeatedly with that b transition. So you get the term ((a+b)a*b)(b+a((a+b)a*b))*. Hope i am clear enough...