div coordinates skewed after rotation

[Violet_82]

Hi guys I wonder if you can help me with this as it's driving me absolutely crazy.
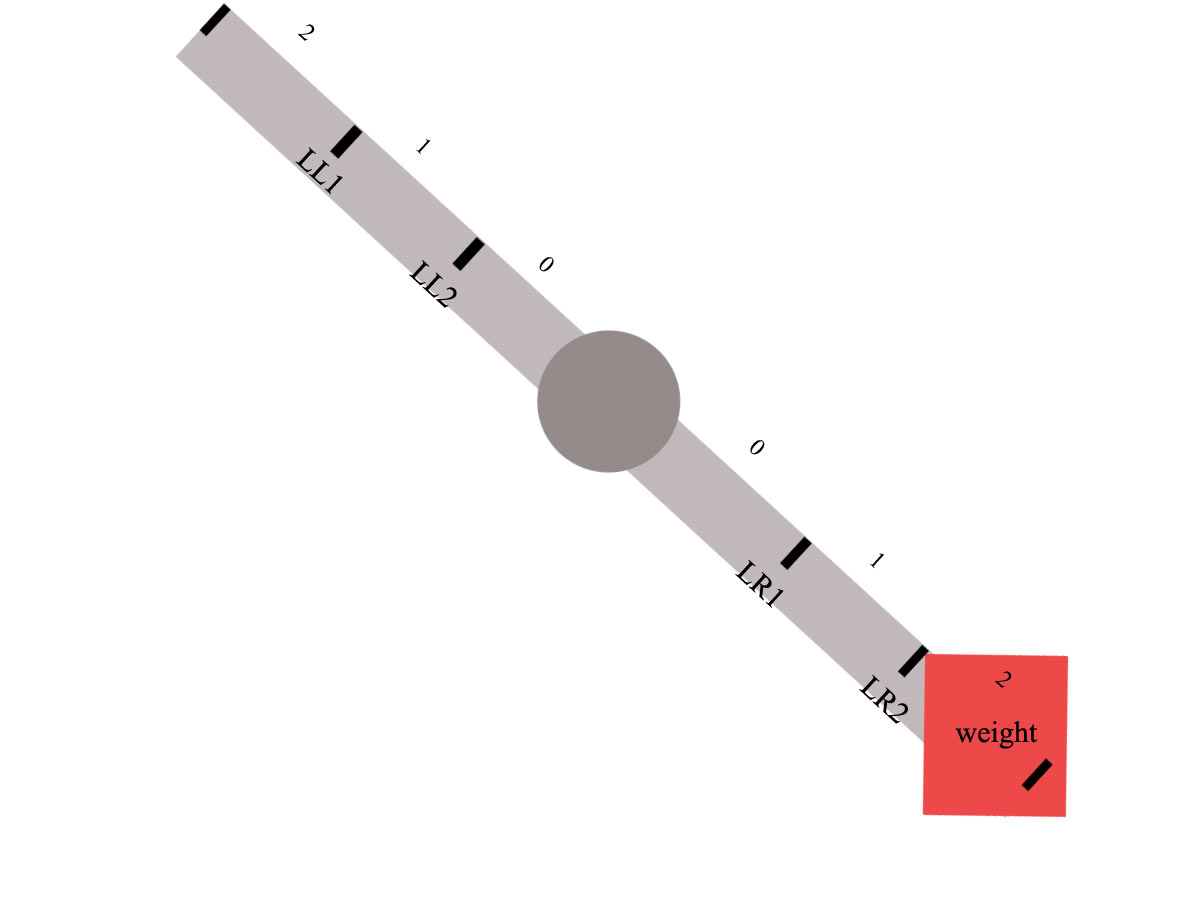
So, I have a div, in the first screenshot which looks pretty much like a scale and can be rotated right up to 45 degrees and left up to -45 degrees

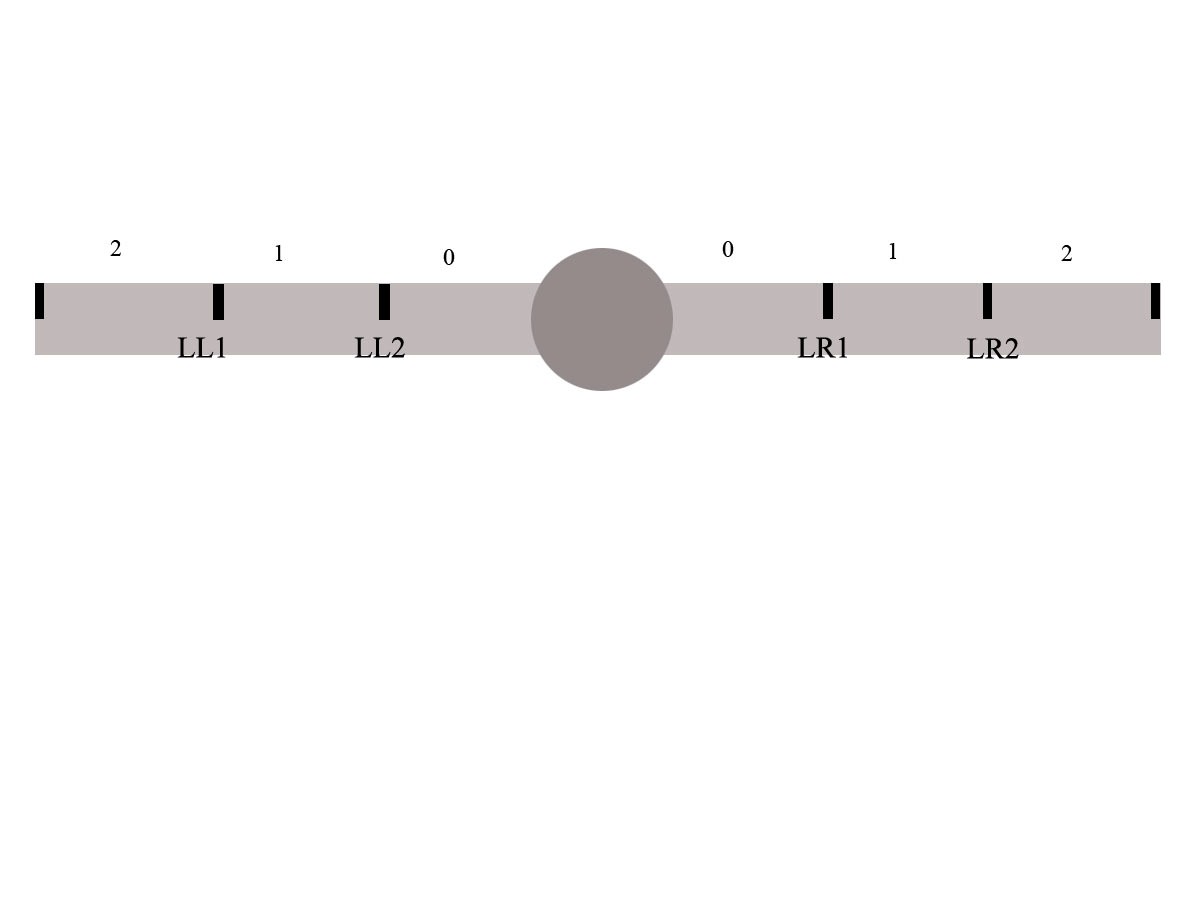
The rotation occurs when something (a div) is dropped on the arm and based on the properties of this div the rotation is worked out and takes place. Of course there can be lots of divs in the scale, but here for the sake of simplicity we'll see only one.
Now, I set some limits as you can see, because when something is dropped on this scale I need to know in which section (0,1,2) of which side of the arm, the weight is.

LL1 = $(".arm").offset().left + this.unitSize;//where unitSize is the width of section 0,1,2 etc and arm is the actual horizontal div
LL2 = this.LL1 + this.unitSize;
LR1 = $(".arm").offset().left + ($(".arm").width() / 2 + $(".pivot").width() / 2 ) + this.unitSize;//I need to make sure I exclude the pivot
LR2 = this.LR1 + this.unitSize;

So, these limits, the first time, are worked out at the beginning before the rotation takes place as part of the initialization, so when the angle is 0.
When the arm rotates though I need to recalculate them, and that's where I'm having loads of problems because, after the rotation, the coordinates of the limits do not match the coordinates of the divs dropped off onto the limits on the scale.
Let me give you an example, let's take this screenshot:

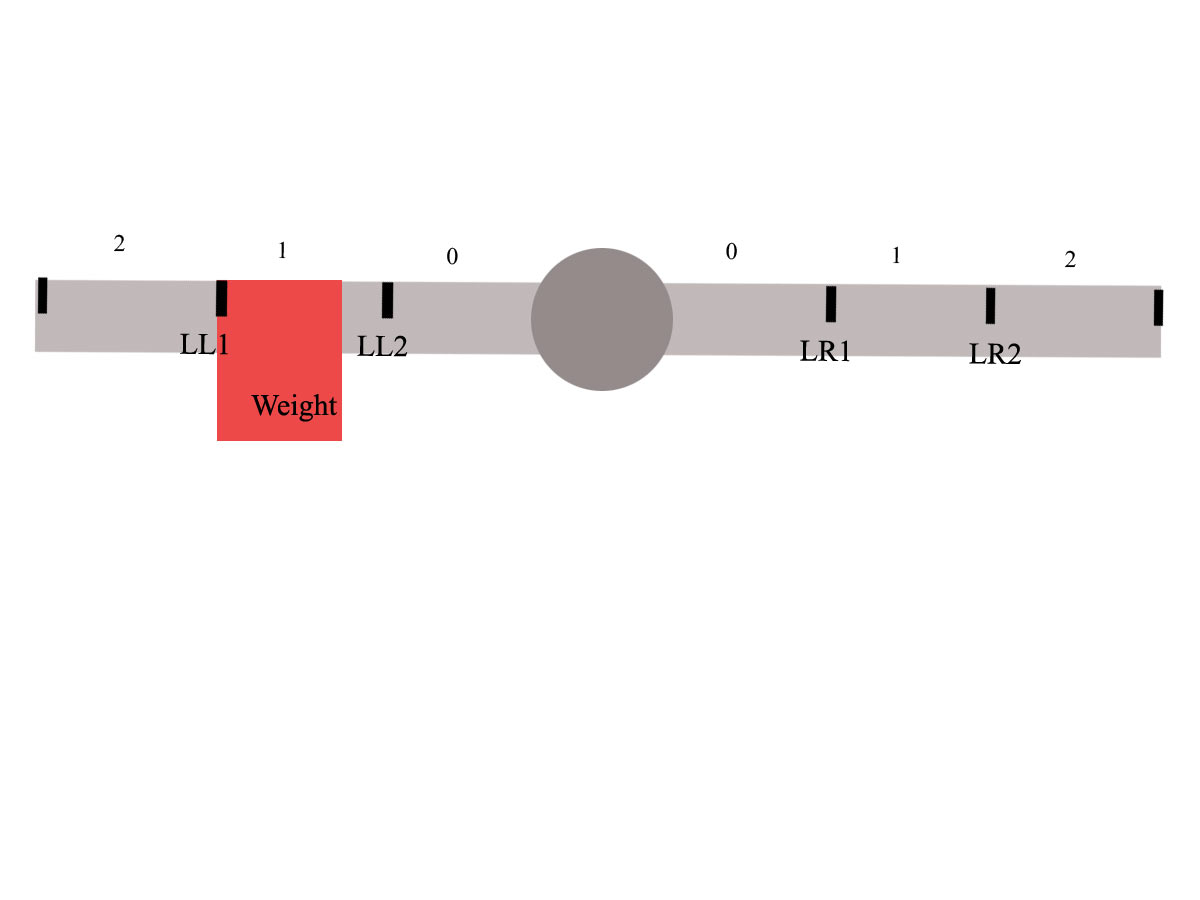
The rotation angle here is 0 so the left coordinates of the weight (worked out with getBoundingClientRect().left) are, at my resolution, 478.
The weight is on the tick, well just about, and the coordinate of LL1 here are of course 478.
Now, let's say the arm rotates about -45 degrees and ends up like this:

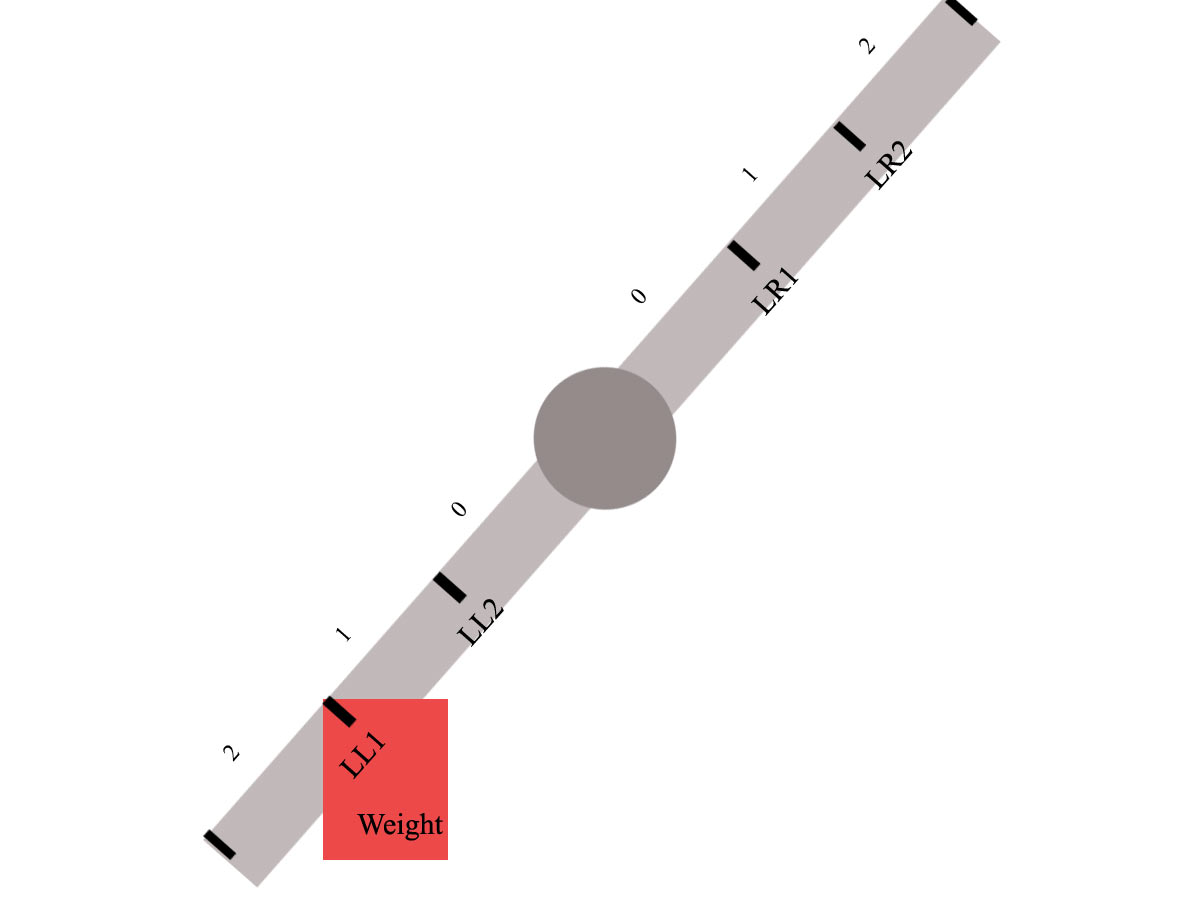
the left coordinates of the weight are now 523.69482421875 because of the rotation. Now I have to update the LL1 limit, to make sure that my limit too is set to 523.69482421875 or thereabout because I need to verify that that weight sits in fact within the LL1 limit (the same goes for all the other limits of course and when a weight is dropped on the limit the coordinates of this weight must match the limit).
I tried various things but the limits are always invariably larger (or smaller depending on the calculation) than they should be, sometimes a couple of pixels, which it's fine, and sometimes 60 or 70 pixels, which is not good at all.
I read a few posts about sin and cos but alas maths isn't my thing really, so I got a little lost and tried to get some ideas from there, but still no joy
Here is what I have attempted so far with explanation when I can give one :-)!
All the below occur after the rotation of course and are an attempt to update the limits:
1)

LL1 += (offset of arm when rotation is x degrees) - (offset of arm when rotation is 0 degrees ) 
LL2 += (offset of arm when rotation is x degrees) - (offset of arm when rotation is 0 degrees ) 
LR1 -= (offset of arm when rotation is x degrees) - (offset of arm when rotation is 0 degrees )  
LR2 -= (offset of arm when rotation is x degrees) - (offset of arm when rotation is 0 degrees )  

This because I thought that the difference between the two offsets added to the left limits and subtracted from the left limits will make out for the fact that the width of the divs 0,1,2 was shorter when the arm was rotated, but no joy, I still couldn't get the left coordinates of the weight when dropped like in the previous screenshot to match the coordinate of the LL1

2) I also tried some variations of the above, like adding that offset to all the limits, subtracting from all the limits and the opposite of above, no joy

3)

var postRotationTickWidthDiff = scale.ruler.unitSize - Math.cos(degrees * (Math.PI / 180)) * scale.ruler.unitSize;

here I had an idea. The width of the 0,1,2 divs is fixed of course, so I calculated the difference between when they are at rotation 0 (unitSize) and when they are instead at rotation 'degrees'
Then I had:

LL1 += postRotationTickWidthDiff
LL2 += postRotationTickWidthDiff 
LR1 -= postRotationTickWidthDiff  
LR2 -= postRotationTickWidthDiff

this worked better, in the sense that the difference between the two coordinates (limit and weight dropped on the limit) were smaller, but still not good

4)Obviously I tried a few variations of the above
5)

LL1 += (offset of arm when rotation is x degrees) - (offset of arm when rotation is 0 degrees ) - (postRotationTickWidthDiff/2)
LL2 += (offset of arm when rotation is x degrees) - (offset of arm when rotation is 0 degrees ) - (postRotationTickWidthDiff/2)
LR1 -= postRotationTickWidthDiff  
LR2 -= postRotationTickWidthDiff

Here I was just experimenting.
So, is there a formula I can use to work out what the limit should be increased to when the arm rotates? The goal here is that if a weight is dropped on a tick as that's a limit, the left coordinates of the weight have to match those of the limit, otherwise there is no point having limits in the first place. I hope I managed to explain myself.
I hope you guys can put me on the right path please.
Here is another scrennshot showing rotation on the other side:

[JamesCherrill]

I have no idea what the answer is, but this post gets my vote as the best question of the decade. If only all our questions were so clear, so well explained, showed so much effort...

I really really really hope someone can help

[Geoff_3]

If I understand the problem, I think that the formula you require is y = cos(a) * x where...
a is the angle (in your example 45 degrees)
x is the distance from the weight to the pivot point (478 in your example)
y is the distance from the weight, after rotation, to a vertical line running through the pivot point - from this you can calculate whatever horizontal distances you require by simple addition/subtraction

I have drawn a simple diagram which hopefully makes it clearer - it is at http://www.kgweb.org.au/pivot.gif
In the diagram the angle is shown with the greek letter theta. Pythagorus has told us that cos(theta) = y / x and rearranging this equation gives us the one I have shown above.

I hope that this what you need to know.

[Violet_82]

thanks for the kind words @JamesCherrill :-)
@ Geoff_3, thanks for the post and the formula. Let me see if I understood correctly what you're saying. With your equation in mind, would my limits be:

LL1 += cos(a) * x
LL2 += cos(a) * x
LR1 -= cos(a) * x  
LR2 -= cos(a) * x

Also, I recalculate the limts after the rotation so x would be the new distance between the weight and the pivot after the rotation has taken place. Correct?
thanks

[Violet_82]

@Geoff_3, in addition to the above, I also thought about an issue. The above formula, I presume, will work when I move a weight around the scale or add one, which is great, but there is also one more thing. As I mentioned before the limits are initiallly set before the animation takes place, when the angle is 0, but there might be already a few weights on the scale, like, preset weights if you like, which means that the limits needs to be updated.
So, if a weight is dropped on the scale - either because it's created or because it's moved - then I can use the data from that weight to work out the limits (using the formula because I can find out how far the weight is from the pivot) but when there are, say, 6 weights on it to start with and I need to work out the limits, as the formula asks for the distance between a specific weight from the pivot, it won't work as there are 6 weights on it ? Do you know what I mean?

[Geoff_3]

Hello Violet_82
Sorry for the delay in replying - demolishing a house has been taking all my time.
I am not sure that I understand exactly what you want to do, but the formula I provided can be applied generally. I am assuming that, based on whatever weights are on the arm at any given time, you know the angle of the arm to the horizontal at that time. Using this value the formula will give you the horizontal distance to the extent of the pivot point from any point (defined by the distance along the arm to the pivot point) on the arm. So if you have, say, two limits then you can calulate a value for each limit.
Does this help?