Introduction

This tutorial provides guidance on gathering data through web-scraping. However, to demonstrate the real-life issues with acquiring data, a deep-dive into a specific, complicated example is needed. The problem chosen, acquiring the geographic coordinates of gas stations in a region, turns into an interesting math problem that, eventually, involves "sacred geometry".

Application Programming Interfaces (API's)

No matter which Data Science Process model you subscribe to, actually acquiring data to work with is necessary. By far the most straightforward data source is a simple click-to-download in a standardized file format so you can utilize a parsing module in your favorite language; for example, using Python’s pandas.DataFrame.from_csv() function parses a .csv into a DataFrame object in one line .

Unfortunately, it’s not always this easy. Real-time data, like the stream of 6000 tweets per second, can’t simply be appended to an infinitely-growing file for downloading. Furthermore, what happens when the dataset is extremely large? Smaller organizations might not be able to provide several-gigabyte downloads to each user, and if someone only needs a small subset, then giving them everything would be inefficient.

In general, these problems are solved through an Application Programming Interface (API). API’s are a programmer’s way of interfacing with an application, or in the context of this article, the means by which we will acquire data. Here's a great, concise resource on why API’s are needed .

One quick note. API’s are typically different from one another, so it’s not necessary to learn every detail, and are you not expected to. You’ll gain experience by using them.

To see how data gathering can look in practice, this article will demonstrate a hands-on approach to find and deal with an API I’ve never used before.

Find the Data Source

Before any searching, specify your intentions. For our case, the goal is to get the location, latitude and longitude, of gas stations in the United States in a Python pandas.DataFrame. Notably, it took some googling life hacks to find a free, comprehensive source that meets our requirements. It’s a little old, but myGasFeed.com has the data we’re looking for.

myGasFeed was an API a developer would use to get the local gas prices of an area for a website, mobile app, etc.

Read Rules & Guidelines

Anytime you acquire data programmatically, look for any rules somewhere on the website. They might require you to register for an access key, limit requests, cite them, or follow some uncommon procedure for access. As a data-seeker, you should read pay attention to guidelines for practical, ethical, and potentially legal reasons. Often, the practical part is a tutorial for accessing the data.

In myGasFeed’s about page, they describe its features and technology, but also inform that the data is freely accessible through their API. It also refers you to the API section that has directions on how to use a generic API key to access the data.

Hands-on Data Acquisition

Start Small, Then Scale

We need to write a program that interfaces with the myGasFeed application, that is, we need to use its API. In myGasFeed's API requests directions, they provide a developer API key to use outside of a production environment. There's also a template URL to request all the gas stations in a certain radius, centered at a specified latitude/longitude. The response will be in JSON format.

Our program must generate the URL for a query, make a request for the data at that URL, then parse the response into a pandas.DataFrame.

First, a function to generate the URL requires a starting location, query radius, type of fuel, sorting criterion, and the API key. New Orleans, Louisiana will be our first example, but you can use any U.S. location you'd like. Just be sure that you put negatives in front of latitude if given in degrees South, and longitude if given in degrees West.

def make_url(lat, long, distance, fuel_type, sort_by, key="rfej9napna"):
    url = "http://devapi.mygasfeed.com/"
    url += "stations/radius/%s/%s/%s/%s/%s/%s.json?callback=?"%(lat, long, distance, 
                                                                fuel_type, sort_by, key)
    return url

nola = (29.9511, -90.0715)
gas_stations_url = make_url(*nola, 40, "reg", "price")

The content of the gas_stations_url is the string
'http://devapi.mygasfeed.com/stations/radius/29.9511/-90.0715/40/reg/price/rfej9napna.json?callback=?'
and represents the URL to request all gas station data within 40 miles of the center of New Orleans. Note that "reg" corresponds to regular gas, "price" means the gas stations are sorted by price, and the requested radius must be less than 50 miles.

Next, we have to actually request the data using the well-named "requests" module. With it, we can send a "GET" request to a specified URL with the requests.get function. The myGasFeed API allows for GET requests, so it knows how to send data back to our variable.

import requests

response = requests.get(gas_stations_url, 
                        headers={"user-agent":"Jeffrey Lemoine, jeffmlife@gmail.com"})

Notice that the headers parameter has my name and email. This is not necessary but is good practice; for someone checking for malpractice, a name and email might convince them you're not a bot.

The response variable is a requests.models.Response object. The data we requested is in the text attribute. Let's check by printing the first 100 characters in the response text.

print(response.text[0:100])

prints

 '?({"status":{"error":"NO","code":200,"description":"none","message":"Request ok"},"geoLocation":{"country_short":null,"lat":"29.9511","lng":"-90.0715","country_long":null,"region_short":null,"region_long":null,"city_long":null,"address":null},"stations":[{"country":"United States","zip":"70458","reg_price":"N\\/A","mid_price":"N\\/A","pre_price":"N\\/A","diesel_price":"3.85","reg_date":"7 years ago","mid_date":"7 years ago","pre_date":"7 years ago","diesel_date":"7 years ago","address":"3898 Pontch'

Though messy-looking, it appears we received a valid response since there were no error codes and the request is said to be "ok." However, the JSON response is wrapped between '?( and )'. This can be solved with a short function to parse responses into a valid JSON string.

import json 
def parse_response(response):
    # get text 
    response = response.text

    # clean response text
    # initial response is wrapped in '?(...)'
    response = response[2:][:-1]

    # make json 
    data = json.loads(response)["stations"]

    return data

json_data = parse_response(response)

json.loads requires the JSON standard, so trimming the response is necessary to prevent a JSONDecodeError. Since we are interested in gas station locations, only the "stations" values of our response are required. The return type of parse_response is a list of same-keyed dict's. For example, a random element in json_data has the dict

    {'address': '1701 Highway 59',
     'city': None,
     'country': 'United States',
     'diesel': '1',
     'diesel_date': '7 years ago',
     'diesel_price': 'N/A',
     'distance': '29.2 miles',
     'id': '73100',
     'lat': '30.374134',
     'lng': '-90.054672',
     'mid_date': '7 years ago',
     'mid_price': '3.49',
     'pre_date': '7 years ago',
     'pre_price': '3.61',
     'reg_date': '7 years ago',
     'reg_price': '3.29',
     'region': 'Louisiana',
     'station': None,
     'zip': '70448'}

Everything checks out (except that the data is outdated 7 years).

Thankfully, a list of dicts can be transformed into a DataFrame in one line, but some more processing is required.

from pandas import DataFrame, to_numeric

gas_stations = DataFrame(json_data)[["lat","lng"]]
gas_stations.columns = ["lat","lon"]
gas_stations["lon"] = to_numeric(gas_stations["lon"])
gas_stations["lat"] = to_numeric(gas_stations["lat"])

In that same line, only latitude and longitude columns were included. Then, the columns were renamed because I don't like "lng" as a shorthand for longitude. The coordinate values were converted from strings to numbers. The final DataFrame looks like:

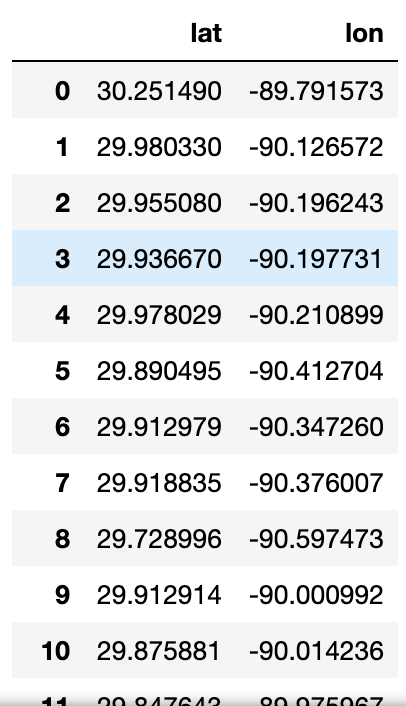
and has 465 rows.

Voilá! We now have the geological coordinates of gas stations within 40 miles of the center of New Orleans. But wait, we only used a 40-mile radius and are limited by 50 miles, what if you wanted more? The next section will take our small example and scale it to any radius.

A Naïve Solution

Here's our problem: we can only request locations less than 50 miles from a specified center in a single query but want locations more than 50 miles away. We also want to minimize queries to be respectful to myGasFeed.com, and because we programmers strive for optimal code. I figured that we should choose different centers such that there is minimal overlap between radii but still encompass all space. Since we're dealing with circles it's impossible to avoid some overlap, but we can try to minimize it.

Let's use Denver, Colorado as our new center and draw a circle with a 49-mile radius around it.

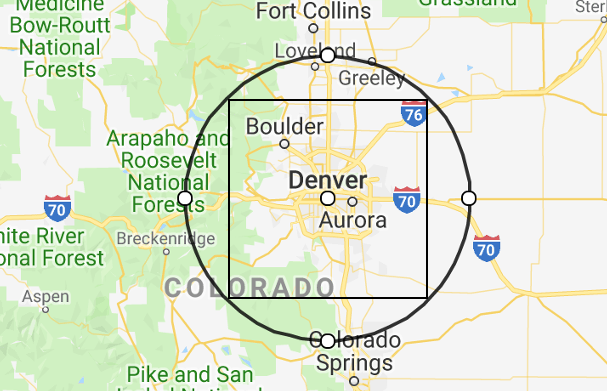
Our previous code can already find all the gas stations within that radius. Next, we will figure out a way of generating centers that increase coverage. The naïve, but simplest, approach is to expand the centers outward in a gridlike fashion. The distance between centers can be the circle radius (49 miles) times the Euclidean distance on a grid. Each of those centers is a separate query to myGasFeed, so the data will need to be consolidated.

Now, let's write the function to generate the naïve grid before we make things more complicated. The procedure is simple. First, make an n x n grid. Then, for each square in the grid (there will be n^2 of them) calculate how far it is from the origin, as well as its angle with respect to True north. With a starting coordinate (Denver) and the distance and direction of a grid point, we can calculate where on Earth that point would be.

from numpy import *
from numpy.linalg import det 
from itertools import product 
from geopy.distance import geodesic, Point

def angle_between(v1, v2):
    """Calculates angle b/w v1 and v2 in degrees"""

    # dot product ~ cos(θ)
    dot_product = dot(v1, v2)     
    # determinant ~ sin(θ)
    determinant = det([v1, v2])    

    # tanθ = sin(θ)/cos(θ) ==> θ = arctan(sin(θ)/cos(θ))
    angle_radians = arctan2(determinant, dot_product)  

    # Convert to degrees in [0,360)
    return (angle_radians * (180 / pi)  + 360) % 360

def expand(center, radius, n_radii):

    # Define starting point
    start = Point(*center)

    # Generate square grid of shape (n_radii x n_radii)
    rng = arange(start = -n_radii, 
                 stop = n_radii + 1, 
                 step = 1, 
                 dtype = float64)
    grid = list(product(rng, rng))  

    # Remove center square [0,0]; no calc. required
    grid.remove(grid[len(grid)//2])

    # Reference direction 
    true_north = array([0,1], dtype=float64)

    new_centers = [center]
    for square in grid:
        # Calculate clockwise angle of square center wrt.
        # true North in degrees [0,360)
        bearing = angle_between(square, true_north)

        # Calculate distance to travel 
        euclidean = lambda p1, p2: sqrt(sum((p1-p2)**2))
        dist = radius * euclidean(square, array([0,0]))

        # Find coord. of point *dist* miles away at *bearing* degrees
        # Using geodesic ensures proper lat, long conversion on ellipsoid
        lat, long, _ = geodesic(miles = dist).destination(point=start, bearing=bearing)
        new_centers.append((lat, long))

    return new_centers

points = expand(denver, 49, 1)

Admittedly, my first version of expand code could only expand once to produce a center at every 45º, or a 3 x 3 lattice of points. When attempting to expand to additional radii, calculating the angle with respect to true north (i.e., the bearing) had to be generalized, which is what angle_between addresses; if you're interested in how angle_between works, check out its linear algebra here.

As for the details of expand, it's sufficient to read its comments for an understanding. Long story short, points contains a 3 x 3 naïve grid of coordinates centered at Denver, scaled by 49 miles. If we plot these coordinates with their respective circles, we can see substantial overlap.

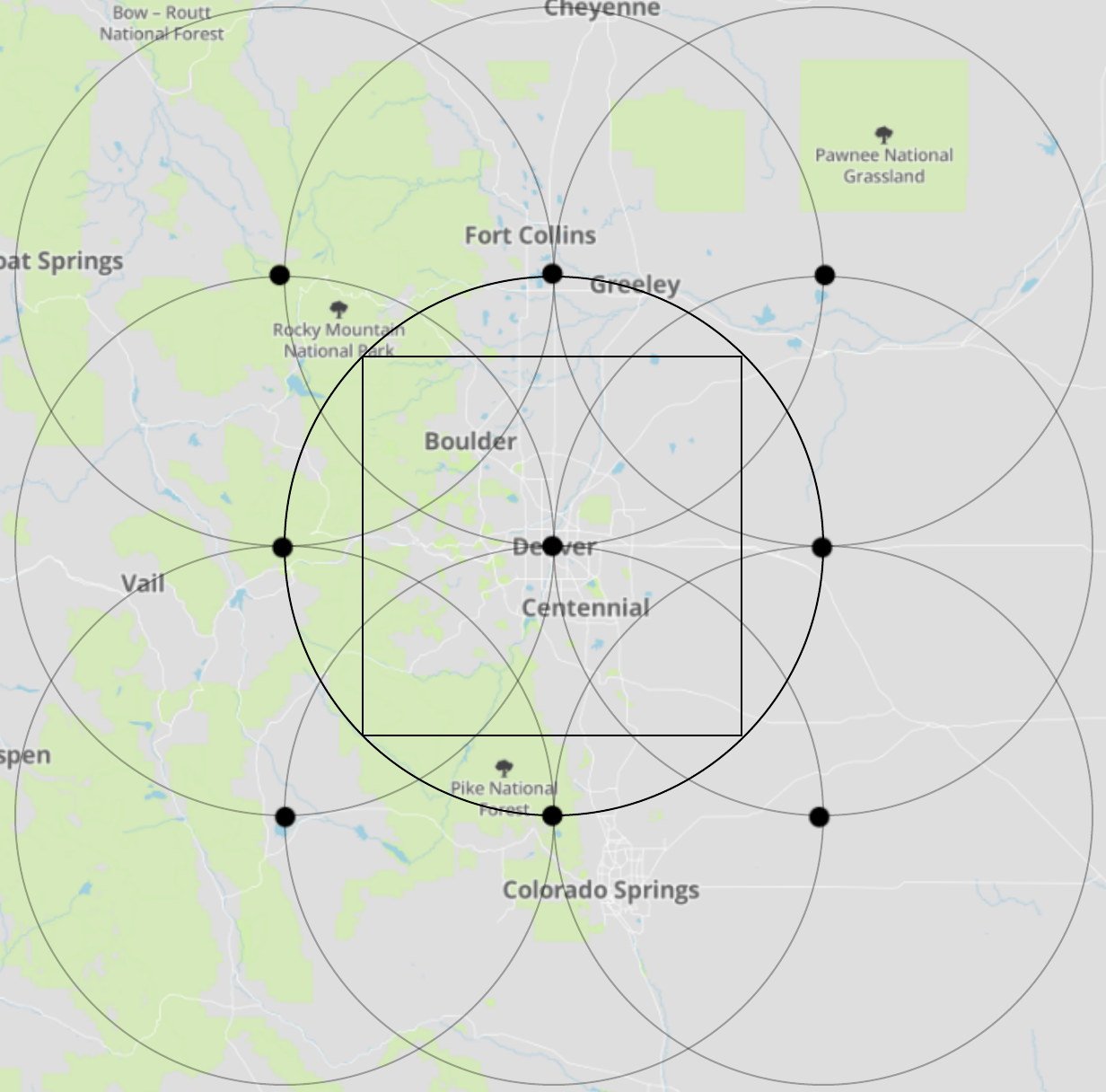
While the naïve grid indisputably achieves more-than-full coverage of the area, it's visually apparent that the grid is too tightly-spaced. Thus, there should be a number we can multiply the grid space with to maximally separate the circles without missing any space. But which number?

The Optimal Grid

The solution for how to best distance the grid points for minimally sufficient circle overlap was surprisingly quite simple. Notice that within the center circle of the naïve 3x3 grid image (above) there was a square. Its diagonal is equal to the diameter of the circle; therefore, it's the largest possible square that can fit inside a circle with that radius. Interestingly, when I put the squares inside the other circles, even they overlapped inside the naïve grid.

We can visualize the inner square overlap through the following color scheme: green for no overlap, yellow for two squares, and red for four squares.

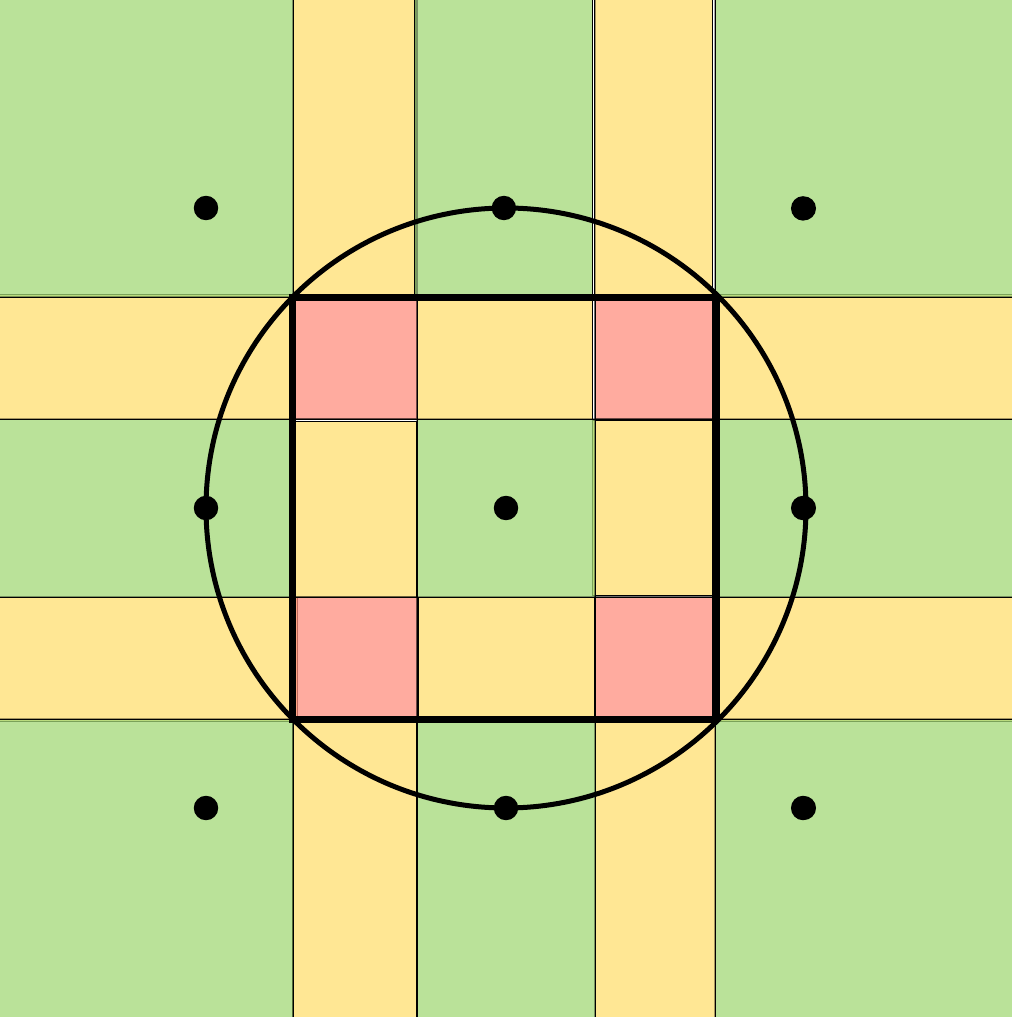
What happens if we were to minimize the overlap between maximal squares such that all inner space is still covered? It would just be a grid of squares and, under our previous visualization, they'd all be green squares. Most importantly, it turns out that organizing circles in a grid according to their maximal inner square is the optimal grid for minimizing circle overlap (and maintaining full coverage).

I will now informally prove this. Imagine a grid of squares. At each corner, there are four squares surrounding it making a cross. If you were to nudge the bottom left (blue) square towards the center (red arrow), additional overlapping occurs; if you were to move the square away from the center (green arrow), then you'd lose full coverage.

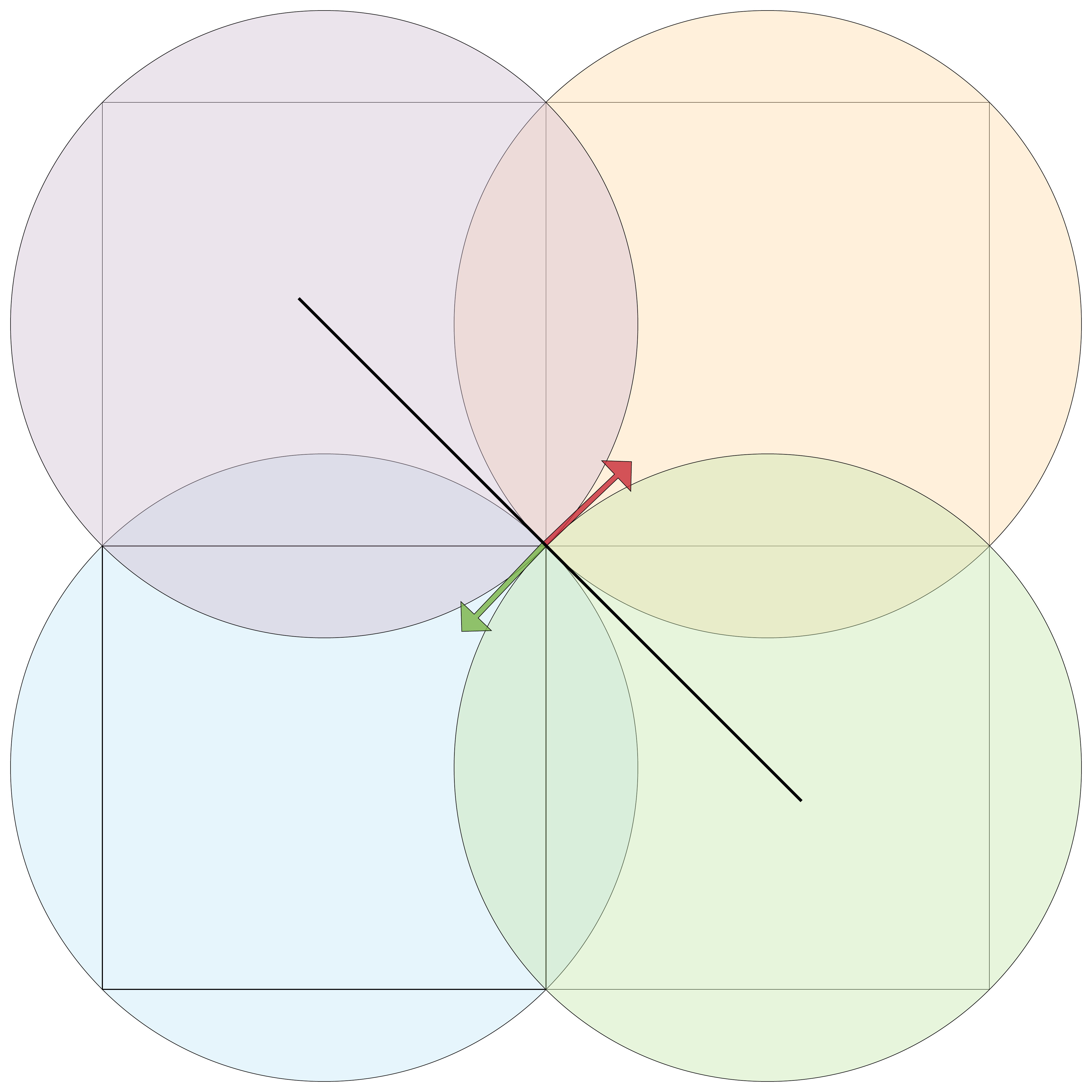
While it's hard to see, moving the blue square away from the center really would lose coverage. To grasp this, look at the black line between the blue and the orange circle. There is only a single point, at the center of the grid on their square's diagonal, in which they touch this line. This is equally true for the rest of the circles. Therefore, any movement away from the circle would not be full coverage.

Even more, this logic applies to the whole grid because traveling along the green arrow for one center, is a red arrow at another (except for the edges).

Implementing the Solution

To actually implement the optimal grid, all we need to do is find the scaling factor for our grid space. Recall that the naïve grid's number, the circle's radius, was too small. Also, we already know the radius of the circle. We are missing the maximal square's dimension, x, which we've shown is the scaling factor we require.

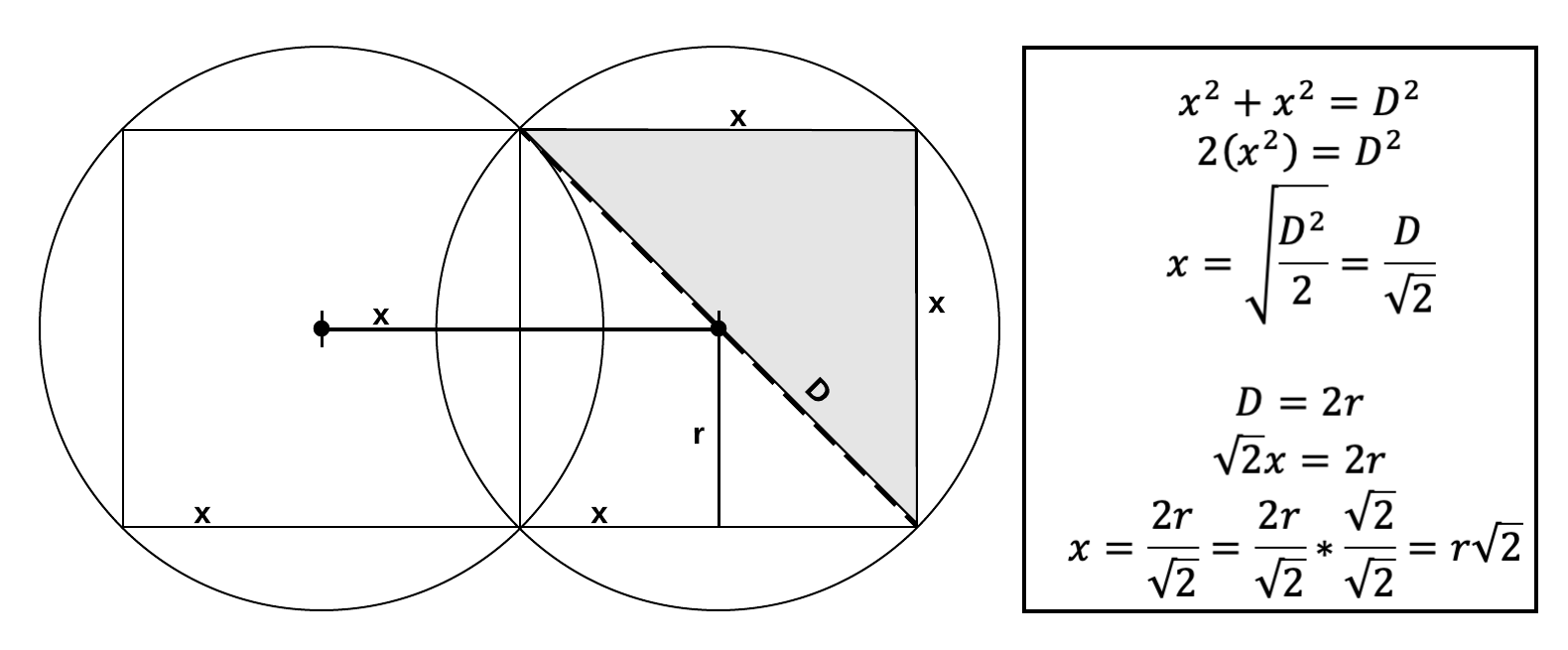
The optimal grid's scaling factor is the square root of two (~1.414) times the radius of the circle. It separates our grid space such that the circles of that radius have their maximal squares lined up, and their overlap minimized.

All we have to do to our original expand function is multiply the distance to travel by the square root of two:

...
dist = euclidean(square, array([0,0])) * radius * sqrt(2)
...

Now, a single expansion looks like:

The Final Scrape

The expand function only generates coordinate centers that we need to query. A new function is required that can query all the new points. Although, this time we need a way to deal with failed requests, as well as the rate at which we request.

The procedure is as follows. First, generate the list of URL's to process from the points returned from expand, and put them in the list to track whether or not they've been processed. When that list is empty, return the responses. All that "process" means is to use our earlier function, parse_response, and store its result.

from time import sleep 

def query(points):
    # List of URL's that need to be processed
    to_process = [make_url(*point, 49, "reg","price") for point in points]

    # Current url to process 
    url = to_process.pop()

    data = {}
    while(to_process) :     
        response = requests.get(url, 
                                headers={"user-agent":"Jeffrey Lemoine, jeffmlife@gmail.com"})

        # try to parse, except when bad response
        try: 
            json_data = parse_response(response)
        except (json.JSONDecodeError):
            # Push failed url to front 
            to_process = [url] + to_process
            continue 
        finally: 
             url = to_process.pop() 

            # Limit requests to one per sec.
            sleep(1)

        print("\r%d left to process"%(len(to_process)), end="")
        data[url] = json_data

    return data 

json_data = query(points)

Inside the while loop, there is a try-catch-finally statement that ensures proper handling of a bad request; if there is a bad request, the response is not our JSON data, so it would throw a json.JSONDecodeError when trying to parse it. When a request fails, we don't want the loop to iterate and try that same URL over and over again, so we push the failed URL to the front of to_process. Finally, (that is, after either a successful or a failed request) pop the end of to_process, and sleep one second so that we are respectful to the server.

And, with just a little more processing...

from itertools import chain

stations_list = list(chain.from_iterable(json_data.values()))

gas_stations = pandas.DataFrame(stations_list)[["lat","lng"]]
gas_stations.columns = ["lat","lon"]
gas_stations["lon"] = to_numeric(gas_stations["lon"])
gas_stations["lat"] = to_numeric(gas_stations["lat"])
gas_stations = gas_stations.drop_duplicates().dropna()
gas_stations.index = range(len(gas_stations))

We are back to a DataFrame with our data in the proper numerical types. Since the circle's we generated had overlap, a drop_duplicatescall is necessary to get unique data points.

Conclusion

The experience gained from this procedure is important to highlight. Not all data acquisition is as straightforward as a click-to-download, or as convoluted as the type seen in this article. Often, you are not given instructions on how to do get the data you need in the format you need it, so some hacking is required to meet your needs. On the other hand, you should ask around, or email a data provider, before you spend hours trying to get an API to work the way you'd like; there might already be a way, so don't "reinvent the wheel" unless you have to (or unless you're writing a tutorial on gathering data).

Notes

It turns out that the problem we formulated, minimizing overlap between a grid of circles, is already an artistic concept (specifically in "sacred geometry"), with its own Wikipedia page. Furthermore, I should emphasize that the optimal solution we found is only for a square lattice. There are other constructions with different grids. For example, a triangular grid with 19 circles :

I encourage you to figure out what the optimal configuration of circles with any underlying grid space (I actually don't know yet), and see if you can code it up.

If you like the images I generated, I used plotly's mapbox for plotting points on a map, and Lucidchart for drawing on them.