A discrete math problem

[Asif_NSU]

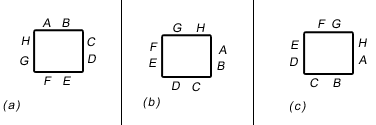
1) How many ways can eight people, denoted A,B,.....,H be seated about the square table shown in the following figure where figure (a) and (b) are considered the same but are distinct from figure (c)?

[IMG]http://imagesavers.com/040927/1096305491.gif[/IMG]

2) If two of the eight people, say A and B, do not get along well, how many different seatings are possible with A and B not sitting next each other?

My answers were (1) 5,040
(2) 3,600

Dont know if my answers are correct, if u think it's not could u plz solve it for me? better if with explanations. Thanx.

[jasweb2002]

Well, how did you get those answers?

[Asif_NSU]

Well, how did you get those answers?

this way:
a) Lets imagine A fixed in a position like in figure (a), then we have 7 letters to fill up the 7 spaces around it, thus 7! = 5,040. It's like a circular table where number of permutation of 8 objects is 8!/8 = 7! = 5,040. I m unsure if i m correct.

b) Like in (a) i imagined A in a fixed position, then we have two adjacent places around A-- now here i have a confusion, for example lets look at figure (a) where B is adjacent to A, but should i consider H being adjacent to A also? if not then we have only one adjacent place to A to be filled up by any other letter other than B. This way we have 6 x 6 x 5 x 4 x 3 x 2 x 1 = 4320.
However if i consider that in figure a H is also adjacent to A then I get 6 x 5 x 6 x 4 x 3 x 2 x 1 = 3600 (my answer).

If it really tough to convey the idea without visualization , but i tried my best. I might even be doing it totally wrong. want to see if anyone can help.

[Asif_NSU]

Hey guyz, some help with the problem please...

[Asif_NSU]

sorry for the figures not showing up, free image hosting seem to work only for a few days. here's the figure: