Posts by MattEvans

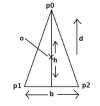
You don't need all the trig stuff, but the principle is OK. See attached diagram for a guide to what each variable in these expressions is. Assuimg your triangle is isocoles; and is defined as having a base ( scalar ), height( scalar ), origin/centerpoint ( point ) and direction ( vector ).

ASIDE: the first thing you should do when using OpenGL is to write or obtain a library for basic vector and matrix operations; it will make your life a lot, lot easier if you do so. See the dif between the vector implementation and component-wise implementation given.

VECTORS:

Given, origin = o, direction = d, base = b and height = h:

  d_n = normalize( d )
  pd_n = perp( d_n )

  p0 = o + ( d_n * (h/2) )
  p2 = o - ( d_n * (h/2) ) + ( pd_n * (b/2) )
  p2 = o - ( d_n * (h/2) ) - ( pd_n * (b/2) )

NOTE: the vector operations normalize and perp will be provided by any math/vector library worth mentioning, they are shown in full in the component method below, though.

COMPONENTS:

Given, origin = o, direction = d, base = b and height = h:

  // this is how normalization looks component-wise
  d_l = sqrt( (d[x]*d[x]) + (d[y]*d[y]) )
  d_n[x] = d[x]/d_l
  d_n[y] = d[y]/d_l
  
  // this is how perp(endicular) looks component-wise
  pd_n[x] = d_n[y]
  pd_n[y] = -d_n[x]

  p0[x] = o[x] + ( d_n[x] * (h/2) )
  p0[y] …

This thread is now closed, since reverse engineering an encrypted script is likely in conflict with the licencing agreement under which that script was purchased.

browsers,wont,usually,break,a,string,unless,it,has,some,breaking,characters,in,it,such,as,spaces,so,either,this,text,will,extend,forever,or,it,will,get,cut,off,depending,on,the,browser,mostly.

this isnt a daniweb issue,it's more of an issue with a convention in the way text is processed/rendered at the client.

that said, it is relatively easy to fix, just run through the uploaded post data and insert extra breaking chracters as required.

There's a big difference between not able and not willing. I'm glad you got your problem sorted; and I hope you learned alot ( about programming ) in the process. There are a few people willing to run other's code and diagnose unspecified problems; but they're few and far between.

If someone can't find something on internet the best way is to go to forums

Er.. not really. The first place to go is google; it'd save a lot of server-space and reader's time on most forums if people just looked up static reference material before even considering asking anyone else anything. Of course; it helps if you have a remote idea about what you're doing in the first place: and if you don't; you should probably be doing something else.

Wel... you probably shouldn't quote the generic families ( serif, sans-serif, cursive, monospace, etc ).. but arial is a system dependant font; ( its a microsoft font ), so, if you want compatibility, you shouldn't use 'arial' as the only font choice in the first place. Use a list like: font-family:'Arial','Helvetica', sans-serif; ^ will use Arial if its available, else Helvetica if its available, else sans-serif ( which is ALWAYS available but usually ugly ). That selection looks 'pleasant' on the widest range of browsers ( since Helvetica is a common Arial-esque font on multiple platforms ).

Slideout1 isn't defined because the browser checks you're using arent working properly: you're either not selecting a browser atall ( likely, since you don't have any kind of 'default' case ) thus you're running no code to select slideout[1-n]; or the way your accessing slideout[1-n] for the selected browser isn't correct. Generally, you should avoid trying to determine the browser and selecting code that way - either determine each capability as you need it ( i.e. test that the objects document.all / [object].style / etc are defined before trying to use those objects specifically ), or use standards ( where they exist ). Since there is a standard for 'getting an element' and 'setting a style', I don't think you'll have problems, or need to use any kind of browser type determination unless your targetting really obscure/archaic browsers. Just use document.getElementById( 'name' ).style.property..

Font-family names can be quoted. Especially, because the the name might contain whitespace, like 'Nimbus Sans L Condensed'. There is no harm in quoting font family names, even if they do not contain whitespace.

What problem are you having with the code? 'I'm having a problem' isn't very descriptive.

What browsers are you targeting? Since most modern browsers support the notion of document.getElementById( ), and the style collection; try using code like:

slideout1 = document.getElementById( 'slideout1' );
slideout1.style. /*etc */

If you want to do this in coldfusion specifically, this is probably the best board to post in. I have removed the duplicate posting of this question in HTML+CSS.

No, you can't do this in any cross-platform way. There's many good reasons why not - for one, a site could launch popups that were difficult to close without using hotkeys or a task manager. The fact you feel that a given window 'doesn't need a titlebar' is a little irrelevant - it's not your choice to make.

If you really want a workaround; use a top-layer absolutely positioned element holding your popup message, with the visibility of the layer controlled via Javascript. It wont be a popup, but it'll look like one.

If you want to make a game engine, learn a decent language. C++ is decent, but learn it well. There are easier languages to start in, but some good C++ libs go a long way - look up SDL and OpenGL, or DirectX. From ( painful ) personal experience - it is time consuming, and you have to make sure that you stay focused on 'the game' rather than 'the engine', cos it's all to easy to end up working on the minor features for months and then ending up way behind schedule on anything that even resembles 'a game'. But, I guess it's rewarding. I've been working on diff self-made engines for at least a year; often I just tear everything down and start from scratch, so, I have very little to show for it ^_-

Modding an engine isnt that expensive.. if you find a cheap/free engine to mod that is. Look at Ogre or Irrlicht - they are free, but maybe not as full featured/easy to use as massive commercial engines.

I've considered that to; but I've never experienced a virus on Linux and wouldn't know where to start finding out if or not I have one. Worrying; if that's the case.

That said, I really stick to only installing things via the package manager ( official sources ), get all the latest security updates, run a firewall, etc. I wouldn't consider myself high risk, although, things happen..

Well, 'disabling' the scroll lock using xmodmap doesn't seem to have had any effect, because the activity of _my_ scroll lock is still 'formally non-deterministic'. It sometimes does nothing for an hour, and then halfway through typing something the light will come on, my cursor selection will be un-workable, and hot keys fire off in whatever program I'm using. Sometimes it'll go away for an hour after I hit the control and arrow keys a few times, sometimes it'll go away and be back in 10 seconds. Hitting control, winkey, and alt key whilst hitting arrow keys always makes it go away; don't ask how I worked that 'solution' out.

Am gonna buy a new keyboard as soon as I get the time to go past a shop that sells keyboards. A pity - since I quite like this one. I'm thinking now ( because of the total randomness of it, and the fact that hitting random keys hard on the other side of the keyboard solves the problem temporarily ) that the keyboard is getting old, and the tracks on the circuit board are worn/confused. I'm not atall sure if that's the case, or even likely, though.

I can boot into Windows and see if I'm getting the same kinda thing there.. but.. I'd rather not wait around in Windows for an hour.

Well, the whole scroll lock/sysrq/break well is pretty clean compared to the main well; I don't use scroll lock or those other 2 keys much in day-to-day workings.

But, really good idea to remove scroll lock from the keymap!! I've given that a try, at the level of Xorg settings, lets hope it works - all I can do is wait until it _doesn't_ happen again :P

It's an old keyboard, so maybe this is a sign I need a new one..

The thing I dislike about A-star is that, when it can't find a path, it degrades to searching the entire space, with a massive memory overhead to boot.. If you're using A-star in a real tile map or graph, where each tile/graphnode is actually represented by some set of properties, consider dropping the 'closed set' / 'open set' idea, and marking each tile as you pass through it ( i.e. by setting a flag in the tile's properties ). It's very much not thread safe to do that, though.

<!DOCTYPE html PUBLIC '-//W3C//DTD XHTML 1.0 Strict//EN' 'http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd'>
<html xmlns="http://www.w3.org/1999/xhtml" xml:lang="en" lang="en">
<head>
<title>Sticky bar thing 2..</title>
<style type="text/css">
.sticky
{
  position:absolute;
  font-weight:bold;
  border:solid 1px black;
  background-color:yellow;
}
</style>
<script type="text/javascript">
//<!--
function get_vertical_scroll( )
{
  if( window.pageYOffset )
    return window.pageYOffset;
  else if ( ( document.documentElement ) && ( document.documentElement.scrollTop ) )
    return document.documentElement.scrollTop;
  else if ( ( document.body ) && ( document.body.scrollTop ) )
    return document.body.scrollTop;
  else
    return 0;
}
function glue( object )
{
object.style.top = ( get_vertical_scroll( ) + 10 ) + "px";
setTimeout( function(){ glue( object ); }, 1 );
}
//-->
</script>
</head>
<body onload="glue( document.getElementById( 'stickme' ) );">

<div id="stickme" class="sticky">I'm gonna stay up here for a while..</div>
<p>
<!--just a load of one `a' per line to pad out the page and force scrolling-->
a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>
</p>
</body>
</html>

This works for me in Opera 9, Firefox 2 and Konqueror 3.5.

It uses a messy polled refresh on the object. I really dislike that method, it makes the 'fixed' bar jumpy and it means theres always a bit of background code running ( more than usual, that is ). I'm not sure if it'll work in IE6.. I tried to put in contingency for all the ( known by me ) ways that a browser can represent 'vertical scroll'.

>> I developed an entire website in IE6 which completed every aspect of W3c and WAI to find that when FF2 and IE7 came out the website fell …

Really not sure if this a hardware or software issue.. My scrolllock seems to have gone AWOL. The indicator LED doesn't light up when I press the scrolllock key; but, occasionally, the LED lights up, stays on no matter how much I hit the scroll-lock key itself, and only turns off after I hit random combinations of keys on the rest of the keyboard ( I'm not sure which ones, but hitting around the Shift/Ctrl/Winkey/Alt area seems to work.. )

Any ideas what could be causing this?

I'm running Mandriva 2007 community edition, KDE 3.5 Free, with the latest stable kernel version ( 2.6.17.16 ); this seems to happen regardless of what program I'm typing in ( examples Opera and KDevelop ). When the scrolllock light is on, I can't do proper selection of text and ( in Opera ) random hotkeys fire when I type -- I guess that's consistent with scrolllock being 'on'.

( as I was typing this it happened again, I'm not sure if occurs on certain key presses, its got me intrigiued.. )

This works for me on Opera 9 and Firefox 2. Can't check on IE7 cause I don't have it. Not sure if it's exactly what you're after - noteably, you'll have problems making the top 'div' fill a proper width-of-page because position:fixed; throws the element out-of the size constraints of the page.

<!DOCTYPE html PUBLIC '-//W3C//DTD XHTML 1.0 Strict//EN' 'http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd'>
<html xmlns="http://www.w3.org/1999/xhtml" xml:lang="en" lang="en">
<head>
<title>Sticky bar thing..</title>
<style type="text/css">
.sticky
{
  position:fixed;
  top:0;
  left:0;
  font-weight:bold;
  border:solid 1px black;
  background-color:yellow;
}
</style>
</head>

<body>

<!--the important bit-->

<div class="sticky">I'm gonna stay up here for a while..</div>
<p>
<!--just a load of one `a' per line to pad out the page and force scrolling-->
a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>a<br/>
</p>
</body>

</html>

Make a non-Windows distribution, provide source code, show pictures of the game.. it worries me to open an .exe file downloaded from an anonymous file server. Also, I couldn't open the .exe if I wanted to, because I don't use Windows...

That 'works' because putting anything on the first line of an XML file other than a DOCTYPE renders the DOCTYPE totally ineffective - it will at best be ignored, and doing something like this should throw a decent XML parser into a 'failed' state. Why would you want to specify a DOCTYPE, if all you want to do is disable it?

Also, not specifying the system identifier for a DOCTYPE ( i.e. the 'http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd' part in the XHTML DT ) turns off the DOCTYPE's effect on a number of browsers, so, that's probably why leaving that part out 'works'.

New-standard DOCTYPES interfere with legacy code and occasionally code written for quirks-mode/nonstandard interpretation; that's to be expected. Get/write modern code, or drop the plans to use a modern DOCTYPE.

To state again, you're not getting any benefit from doing this - if you don't like the effect of the DOCTYPE, remove the DOCTYPE statement completely, and save a handful of bytes in filesize - at your own risk of course.

If I'm honest, I only dishwash once a week when every piece of kitchenware is unusable for any purpose. So, the cutlery is usually jammed in anyway and everywhere it can fit.

I guess I save loads on dishwasher tabs ^_-

Usability standards or technical standards? For technical standards at the client end; just look at up the latest W3C recommendation for XHTML and CSS, and then step back ( at least ) one version to be sure of compatibility on current / popular / most browsers. If it's technical standards at the server, you're king there - pick whatever standard ( or no standard atall ) that works best. Personally, I think XML + XSLT + compiled applications are the way forward at the server.

As for usability standards.. avoid dependance on plugins, avoid really over-the-top graphic and structure intensive pages, follow W3C and WAI guidelines, ignore hype: and you can't go far wrong.

I put everything handle up, except the sharpest knives: I put them blade up - just to tempt fate. Noteably, I always prep and empty the dishwasher standing on one leg whilst blindfolded.

a user calls to tell you that when they try access a folder on the server that they could previously access, they get a message "the link your trying to access is unavailable or missing, try checking your spelling and try again

Ooh! I know this one!

Cause of the problem: Users who can't spell.

Hope that helps.. O_o

Use only the colours from the Web-Safe pallete: http://www.oreilly.com/catalog/wdnut/excerpt/web_palette.html they are supposed to be the same everywhere. I find that I only need to use the websafe pallete with GIFs; other image types ( ie. PNG's ) tend to always look OK... But, transparency with PNGs is a problem in browsers older than or the same age as Internet Explorer 6...

Thread moved; to a board where you're more likely to get the best coverage..

Personally.. I wouldn't worry about uninstalling Windows if it's really playing up - Windows is only a program. Back up all of your data, of course; in a safe place, and virus scan or selectively bring back your data if you think it might be affected with something..

You have nothing to lose if you back everything up, except a cost in time of setting everything back up again.. That said, wait until / if someone responds who knows more about your specific problem..

@Suetan, since the original poster's code is C++, I sincerly doubt that the means for performing a PHP include will be much help... PHP isn't a subset/superset of C++ : PHP is parsed by and interpretted by a C++ runtime engine; if that's what you mean by 'based off of C++'.

@kidprogrammer, it looks good to me. Perhaps some of the stuff in main could be moved out into other functions; but only if it looks like you'll gain any benefit, and not have many costs ( i.e. having to pass more than about 8 parameters to a 10 line function, or a function that's only called from one place is too many costs ).

Also, a minor; you use the windows.h header only for the 'Sleep' function.. That means your program will only compile on Windows machines, even though most of the code is platform-neutral. If you're only targeting Windows, that's fine. There are other ways to do a sleep( n ) though [ i.e, you should be able to use a call to system( "sleep n" ) and thus cut out the dependancy on windows.h ].

PHP itself is a classic example - everytime you write a PHP 'program', you're relying on many developers prior effort to create that big, unsightly ( but admitadly useful ) bag-of-functions that is PHP. Way off topic for the games forum anyway.

Nearly every commercial game these days uses a mega library / engine for all but the highest level areas of code.. As a more appropriate e.g.: very few people try to pass off the OpenGL library as their own work ( except the developers of a given implementation of OpenGL ), but that doesn't mean you can't write a program that uses OpenGL and call that program 'your own', and using OpenGL doesn't make a program, or a programmer less 'good'. At least I hope it doesn't, because personally, I'm glad that I don't have to write a renderer everytime I need to do some 3D work.

Still.. I guess it's subjective.. but in this case, I don't even get the impression that technogeek_42 wants to rip off anyone's code as his/her own. If people are willing to offer technogeek_42 some libraries and/or code, that's their prerogative, if technogeek_42 then goes off and makes 'the best game ever' with what he/she is given - good for him/her.

@ Suetan: it really depends what you call 'stealing', there are some great algorithms out there that exist in or out of code, implementing a given algorithm isn't 'stealing' it, unless it's patented, or otherwise legally restricted; linking against a library of 'great algorithms' is something that many programmers do once or twice an hour. Everytime you use multiplication, you're kinda 'stealing' the algorithm for fast floating-point multiplication in binary.. unless, you do infact rewrite that yourself... that's a silly example, of course, and I guess, it depends on the complexity of what you're doing - but personally, I'll happily at the very least study prior work before jumping in with the long guns.. Everyone ( and thus every programmer ) has their own strong area(s), and you can certainly get more work done if you allow other people to help you in those weaker areas, via algorithms and code examples.

With regard to actually copy-pasting the ( e.g. C++ ) code for a given algorithm.. hey, it certainly takes 'effort' and knowledge to integrate that with an existing codebase, sometimes more effort and knowledge than reading a non-code formal description of the same algorithm and implementing it from scratch. IMHO, you can't make a good ( non-trivial ) program by 'glueing' bits of other people's unrelated programs together, unless you really know what you're doing in the first place.

Look for any information you can find about the A-star graph-search algorithm. It's a heuristic-based best-first search -- it is pretty much the de-facto 2D pathfinding algorithm, and it works well in tile-based maps. This is probably the best introduction to A-star, specifically for tile maps: http://www.policyalmanac.org/games/aStarTutorial.htm

Alternatively, if that seems a little over-the-top ( it can eat memory like you wouldn't belive in big, fine grids with lots of good-looking paths at the begining [ i.e. mazes ] ), consider using http://en.wikipedia.org/wiki/Dijkstra's_algorithm to find all the best paths when the 'game' starts, and store them in a matrix that shows the best path from every cell to every other cell.. that's very fast in-game, but can also result in a massive, permanent structure for the duration of the game. If your obstacles are all 'simple', and they move about, like lots of small rocks or other agents in the way, consider using a steering approach rather than pathfinding; steering is cheap at runtime and free at initialization time, so, use that if and anywhere that you can.

A simple steering approach is always turn left ( or right ): basically; plot a curve ( a series of line segments ) from the start to the end point; every time the line segment intersects an obstacle, add a new line segment to the curve that goes 'left' as close as you can to the obstacle, once the obstacle is 'cleared' add a line segment …

Thread moved to Networking Hardware Configuration: please try to post in the most appropriate forum, because your post has nothing to do with Web Development.

Also, to get the most useful help, please describe the problem in more detail. Read this thread http://www.daniweb.com/forums/thread5722.html for some good advice about the best way to go about getting your problem solved.

Welcome to Daniweb!.

Yuk.. it's a real hack to serve diff pages to diff browsers, especially when using HTTP headers to determine the browser. How many browsers are you gonna target? What happens when the browser version changes? What happens if the browser identifies itself as a different browser? ( that's not farfetched )

Just go for a minimalist design that doesnt put too high a requirement on browser nuances, avoid floats and abs/rel positioning where possible, and you're laughing all the way to the server. Take a look at some 'popular' commercial or organization sites, most are very simple structurally; just neat, tidy and consistent looking. That's probably not what you want to hear, halfway through a project, but, certainly consider it in future.

Also, don't avoid using tables to prove a point - they tend to be identical across browsers - perhaps because they're so 'outdated' they've become well standardized.

This is good reference, http://www.gamasutra.com/features/19991018/Gomez_1.htm there are collision tests for different pairs of 3D objects ( see contents box on the right ). The tests would work in 2D, but, there are even simpler versions of these tests for 2D.

'Separating objects' that have collided is theoretically simple - calculate the magnitude of the velocities of the two objects before the collision, make them proportional ( i.e. turn the velocities into positive normalized weights ) hold on to those for a second =P. Now, calculate the intersection vector of one of the objects into the other object, that's simple, since most static collision tests for convex hull types give you this information for free. Translate both objects by their normalized velocity weight multiplied by the intersection vector, or by the normalized velocity weight times the intersection vector times minus 1; depending on which of the two objects it is, and depending which way you measured the intersection vector.. that works well for immediate separation of illegally intersecting objects. Alternatively, never put objects into intersection - keep them separate by checking that they can move into space before you move them, or use both methods.

Do you have grid/tile based space or not? If you dont, I suggest using some kind of pairwise pruning before checking objects - i.e. not checking objects that can't collide.

All in all, it's quite a complex subject, but there are many simplificiations. In 2D tile based space, it's alot easier …

On a bad day, once or twice a second... Multiple agents may request the use of this algorithm, multiple times during a simulation. A badly configured agent could ask for this algorithm repeatadly ( every 20Hz update cycle ). A well configured agent shouldn't ask for it more than 10 times a minute, but, with multiple agents, they have to stagger the request to this algorithm, or they all ask at the same cycle. Normally that's fine, since the algorithm rarely has more than a 100 x 100 x 1 search space, and secondly, the likely number of iterations is either 100-1000, or exactly 20,000 ( at the cut off ). So, when no worst cases arise, its quite speedy with a small memory footprint, even when a set is used.

It doesn't have to be threadsafe, though, so, I could feasibly re-use any memory I allocate, if it proved to be worthwhile to do so.

In case you're interested, the algorithm in question is the A* graph search in dynamic 3D space, I don't keep a grid/graph of such representing the 3D space, so this structure represents my 'closed list', which is built on the fly by assigning each discrete point in the search space ( at a given resolution ) a unique identifier, the identifiers are just relative 3D co-ordinates of each point in the space, represented as a single index. The identifer of each visited point in the space gets put in the closed list, …

Well, the set/rb tree does get massive if it ever reaches 20,000 iterations. Way more than storing 20,000 discrete spaces as an array of bits.

I think, I'm gonna look into using small arrays again; so... I'm gonna convert each discrete point into a cell index, a word index ( 32 or 64 bit words ) and an offset ( the bit ). If I keep a sparse array of pointers to dynamically allocated arrays of words ( cells ), one cell for every 100 words for example, then the space can grow in blocks of KBs, rather than starting off being MBs. Since it can be sparse at the highest level, all the untouched chunks of 100 words don't ever need to exist - any 'seen' query to those cells is false. It still might turn out that the cells of words that do exist are mostly 0's, though.

I haven't started on the range structure, I'm just toying with the idea, really. If it's always the case that space fills in contiguous blocks of 1s, it might be OK, but, it needs a sizeable logic overhead compared to either a set, or array(s). Also, if space doesn't fill up in contiguous blocks, then it'd be a terrible structure, since it'll have to store 2 values for every detached point. The worst case would then be, assuming 20,000 non contiguous points have been seen, that the size of the structure was 40,000 index types ( potentially 64-bit …

Can you post more of your code? Specifically, which CSS attributes are applied to the table, and to the large content section in the middle? Also, post the markup of the table, if you don't mind.

Hm, I have looked into using arrays of uints with bit indexing, but, the 20,000 limit is the max number of iterations ( the maximum number of numbers, not the maximum possible number ), the bounds for possible numbers gets much higher. The numbers represent 3D points fitted to a given resolution, in all directions. An area of size 100 x 100 x 100 ( with 1 unit per discrete point ) isn't unreasonable, and about the maximum space ever is probably bounded at 1000 x 1000 x 100. That would be 3,125,000 uint32_ts allocated for _any_ operation in that area; even though the actual number of points explored is only ever going to be 20000; that being an artificial limit solely because letting the algorithm run throughout the entire space isn't feasible, but, it has to be allowed to explore any part of the space that it chooses to.

I've looked at using small block allocated arrays of about 100 unsigned ints at a time, starting at around the first number and then potentially expanding in any of 4 directions ( because 0 actually lies right in the middle of the area ); but, the fact that so much space is wasted ( examining the memory shows huge swathes of 0's ), leaves me a little dis-satisfied with that approach.

I'm trying to work out what the best structure is for these requirements.. will happily work on it, just wondering on the best direction to go in / if anyone knows from experience or reason what the best type of storage structure is..

- I 'generate' up to 20,000 integers, and I need to make sure they are unique. I have no desire to keep track of which integers I've seen, as long as I can determine whether I've seen one before, if that makes sense - I don't need to get them back again from the structure.

- I can roughly predict the distribution of the numbers, I know, for example, the possible 'next' numbers after seeing any given number, I also know that the numbers probably expand from a single point, i.e, in 1-D, if the first number is one, the second numbers will be 0 and 2, if the first number is 2, the next ones will be 1 and 3, and so on.. I'm not considering negatives. However, I only have a rough idea that will happen - and, its certainly the case that the next two numbers might be +100 and -100, or any other symetric distance from the first number ( again, negatives can't happen, so -100 would only be possible if the first number is >= 100 ). The numbers don't necessarily start from 0, infact, its very unlikely that the first number will be 0.

At the moment I'm …

Does the Amhric language need a special font installed? Can it be represented in Unicode? Do you want to serve an Amhric page to people physically in Ethiopia, and an English page elsewhere, or do you want to serve an Amhric page to anyone who can view Amhric, wherever they are in the world? Basically, what are the conditions under which a browser 'has the Amhric language'?

Either way, that is, even if you find it's possible to do this ( which it might be ); I would certainly do as MidiMagic said, put a link saying 'English' or a frontpage saying 'Which language would you like?'.

For getting the same header on every page...

- Configure your server for SSI ( server side includes: http://en.wikipedia.org/wiki/Server_Side_Includes ), or Perl / PHP, or anything else that can glue pages together on the fly.

- Or come up with your own search/replace policy. For example, if you write <!--!!$$$HEADER$$$!!--> where you want your header to be in every file, then do a search and replace in all files before uploading them -- its better than maintaining multiple versions of the same code in different files, and you could even automate it. I'm sure Windows must have some kind of search-replace across files, certain editing environments do for sure.

- You could also use Javascript to append a header to each page, although, that's not a great way to do it since its a post-process, and its offloading trivial work onto client machines..

The easiest way to get that look is with a <table> element, especially if you want text in either of the two side columns. Otherwise.. you can do some tricks with background color, etc, to make it look like the other column's are supposed to be that long, or, you could nest the inner column inside a large element that acts like both side columns. Generally, in CSS only, you cant make 2 blocks be the same size when one of them depends on its content for size ( unless those elements are nested inside each other ).

As long as its always the negative of what it should be; you're ok to put in a * -1, you could also try swapping the cos and sin exprs around, so that movex is the sin, and movey is the cos. I wouldn't worry about it, the problem arises when you're using a diferent idea of what up/down left/right and 0 rads is to the maths itself.. In 2D, I always find that 0 rads in a formula ends up pointing over to the right on screen rather than the oft-desired up, but thats easily solved by adjusting the input angle. It's a good idea to establish a convention early on, and encapsulate it away so you can change your easily mind later.

The first two look good; assuming you have a fixed number of columns and that the tileset can then extend "infinately" vertically, and the tiles are given frame indices like:

0 1 2 3 4
5 6 7 8 9
...

If you index your tiles starting from 1... don't : start using 0 as first index, the math will be alot cleaner.. But, if you must use 1-based indexing; subtract 1 from the current frame before working with it in calculations..

One thing I would do; though:

left = (current frame % number of columns) * sprite width
top =[B] int([/B]current frame / number of columns[B]) [/B]* sprite height 

( where [B]int [/B]is whatever the function is in your language to truncate a decimal to an integer - i.e. round by removing the fractional part )

If you're having problems understanding why it works: http://en.wikipedia.org/wiki/Modular_arithmetic

I don't think there is any way to manually specify texturing co-ords for quadrics objects; since you dont even specify their vertex positions. Do they respond to glTexGen though? I have never tried, but I would think that they should..

http://pyopengl.sourceforge.net/documentation/manual/glTexGen.3G.html

Using the Javascript XmlHttpRequest object ( all common modern browsers have it, although it sometimes has a different name ), you can issue a HTTP request to any page or program on your server, and then process XML replies as a DOM structure, or plaintext replies, as plaintext ( the reply from a page is the page content ). So yes, you can; research XmlHttpRequest, and AJAX. If you use the XML method, you avoid having to do any kind of parsing - the DOM is a ready-formed structure that's quite easy to work with.

EDIT: ha.. i wanna rephrase this "it would have the same run-time for any size of n." to; "it would have the same run-time for any input of a given size of n."

Well, sorting wont hurt you; lets put it that way. At the least, you can remove a number of the potential items that really dont help for a given query. You don't have to pre-compute the weights, you could calculate them for every item based on external factors like the enemies nearby, or the player's intrinsic stats, they don't have to be normalized weights either, just numbers that sumarize each item's 'raw usefulness' in a given situation.

That still leaves a problem of multiple items reinforcing/weakening each other. Are there ways you can categorize items and groups of items based on their effects or dependancies? jwenting mentioned specific 'sets' of co-reinforcing items, I can almost think of an optimization if that's the case.. it's based on sorting again; but sorting 'sets' and their subsets in with the other items and then forming and shunting 'shapes' that come in at the top of the lists.. you could only do something like that if there are little finite groups of items that work together, not if all items have effects on all other items. If all items do affect each other; you could certainly pre-compute the 'interconnections' between items/groups, where they may have effects on each other; there may be a route to optimization there.

Do you think you could convert this to a linear programming problem? Have a look at examples of LP problems ( google, wikipedia ).. they can all be solved via a generalized means; but, it …

I don't think it's NP complete, not the example you've given anyway.

If you assign every viable object it's 'score' for a certain requirement, ( i.e. highest protection ); including negative scores if a piece of equipment 'removes protection'... It's just a case of finding the maximum score item for every slot. ( Highest protection is clearly afforded by equipping oneself with the pieces of equipment that afford the highest level of protection. ) If you have multiple requirements (i.e. highest protection and highest damage ), you can use a weighted sum or a rank calculation for each item's 'score'. Generally, I would try to use an statistical method rather than a reasoning method, unless the problem really requires reasoning.

Are there other constraints though? i.e. If a player has N equiped they can't have E equiped, or similar? Or, do you want to reach an EXACT level of protection/damage/etc?

Well, I've stuck with pure-virtual functions in my case, I had to reorganise though. The 'base class' in question ( A ) doesn't have to be extended - It's a helper class that could be constructed to 'help' any instance of another class B, not necessarily only an instance that extends it AND that other class. So, extending a subclass of both A & B such that it can 'help itself' means it needs a reference to its fully-extended B-self.. Virtuals don't work exactly right because then it can only be created to help itself and can't exist without being a B aswell. I got around it by losing the 'help others' aspect and making most of the helper things static with an extra parameter for the B instance to 'help'. The reason I can't implement all that stuff directly in B - B is a template, specialized into C and D, and there are common functions ( that should be members ) in both specializations but not in B itself... Specializing seems to force me to write everything twice unless I do something like this. The idea to have the helper ( common functions ) work on any existing B-like object and not just a C or a D seems nice, but non-essential. I could also have bound the helper to its helpee late.. but.. I didn't want to do that.

Am more worried about other places where I use the result of member functions to provide initial …

base ( super ) classes dont know about their subclasses, they don't generally have a type-safe pointer to the fully extended class..

im using vs 2003.. but, the eg. you gave doesn't show what I mean:

class foo
{
public:
    foo():myself( this ) {}
private:
    foo * myself;
};

int main()
{
    foo f;

    return 0;
}

^^ try that, if you dont mind, when i try i get a:

warning C4355: 'this' : used in base member initializer list

(( i know that's a silly example, but, there are slightly less silly reasons for wanting to do this ))